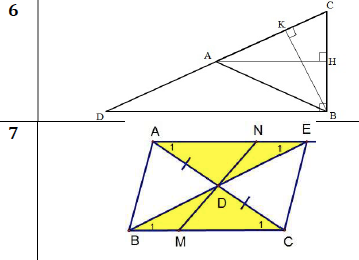
giúp mình tìm các cặp tam giác đồng dạng trong 2 hình này với
Tìm trong hình 34 các cặp tam giác đồng dạng:
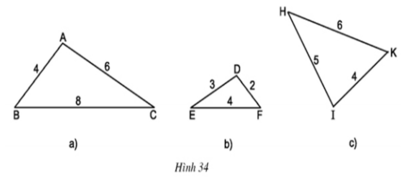
Ba cạnh ΔABC tương ứng tỉ lệ với ba cạnh ΔDFE
⇒ ΔABC ∼ ΔDFE
Tìm trong Hình 4 các cặp tam giác đồng dạng.
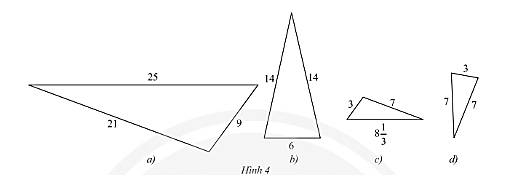
Xét cặp tam giác thứ nhất: Hình a và Hình c.
Ta có: \(\frac{3}{9} = \frac{1}{3};\frac{7}{{21}} = \frac{1}{3};\frac{{8\frac{1}{3}}}{{25}} = \frac{1}{3}\).
Do đó, tam giác ở Hình a và Hình c đồng dạng với nhau.
Xét cặp tam giác thứ hai: Hình b và Hình d.
Ta có: \(\frac{7}{{14}} = \frac{1}{2};\frac{7}{{14}} = \frac{1}{2};\frac{3}{6} = \frac{1}{2}\).
Do đó, tam giác ở Hình b và Hình d đồng dạng với nhau.
Cho hình bên là tam giác ABC vuông tại A, đường cao AH. Trong hình bên có bao nhiêu cặp tam giác đồng dạng với nhau. Hãy chỉ ra các cặp đồng dạng và theo các đỉnh tương ứng.
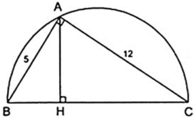
Trong hình bên có 3 cặp tam giác đồng dạng là BHA và BAC; CHA và CAB; HAB và HCA.
Hãy chỉ ra các cặp tam giác vuông đồng dạng với nhau trong Hình 9.52, viết đúng kí hiệu đồng dạng.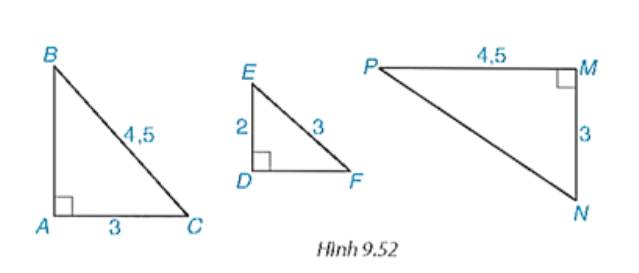
Ta có:
AC/BC = 3/4,5 = 2/3
DE/EF = 2/3
⇒ AC/BC = DE/EF
∆ABC và ∆DFE có:
AC/BC = DE/EF = 2/3
∠BAC = ∠EDF = 90⁰
⇒ ∆ABC ∽ ∆DFE (cạnh huyền - cạnh góc vuông)
Tam giác ABC và tam giác DEF có:
\( \widehat A = \widehat D = 90^0 \)
\( \frac {AC}{DE} = \frac {BC}{EF} = \frac {3}{2} \)
\( \Rightarrow \Delta ABC \backsim \Delta DFE (ch - cgv) \)
Cho tam giác MNP.Gọi D,E lần lượt là trung điểm của cạnh NP,PM. Tìm các cặp tam giác đồng dạng . tìm tỉ số đồng dạng của mỗi cặp tam giác đó. Giải giúp e ạ pls
Xét ΔPED và ΔPMN có
\(\dfrac{PE}{PM}=\dfrac{PD}{PN}=\dfrac{1}{2}\)
\(\widehat{P}\) chung
Do đó: ΔPED~ΔPMN
=>\(k=\dfrac{PE}{PM}=\dfrac{1}{2}\)
Cho tam giác vuông ABC (góc A= 90 độ), đường cao AH. Tìm tất cả các cặp tam giác đồng dạng với nhau có trong hình và giải thích tại sao?
Ở hình 51, tam giác ABC vuông ở A và có đường cao AH.
a) Trong hình vẽ có bao nhiêu cặp tam giác đồng dạng với nhau? (Hãy chỉ rõ từng cặp tam giác đồng dạng và viết theo các đỉnh tương ứng).
b) Cho biết AB = 12,45cm, AC = 20,50cm. Tính độ dài các đoạn thẳng BC, AH, BH và CH.
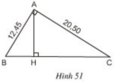
a) ΔABC  ΔHBA vì Â = Ĥ = 90º, B̂ chung
ΔHBA vì Â = Ĥ = 90º, B̂ chung
ΔABC  ΔHAC vì Â = Ĥ = 90º, Ĉ chung
ΔHAC vì Â = Ĥ = 90º, Ĉ chung
ΔHBA  ΔHAC vì cùng đồng dạng với ΔABC.
ΔHAC vì cùng đồng dạng với ΔABC.
b) + ΔABC vuông tại A
⇒ BC2 = AB2 + AC2
(Theo định lý Pytago)

ai đó giúp mình giải bài này với
vẽ hình tam giác ABC vuông góc tạo A, kẻ AD vuông góc AB. chứng minh tam giác AHB đồng dạng với tam giác CHA
cho tam giác abc vuông ở a đường cao ah
1) hày tìm các cặp tam giác đồng dạng có trong hình vẽ
2)chứng minh a)ac2b

a) ΔABC
ΔHBA vì Â = Ĥ = 90º, B̂ chung
ΔABC
ΔHAC vì Â = Ĥ = 90º, Ĉ chung
ΔHBA
ΔHAC vì cùng đồng dạng với ΔABC.
b bn nói rõ ra tí đc ko chứ ac^2b là gì ai hiểu đc