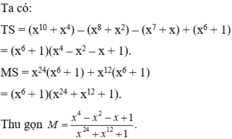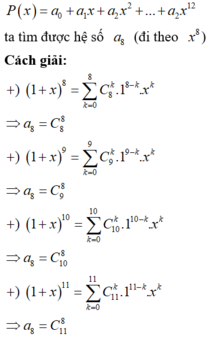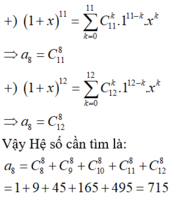Tìm x biết x10 = x12

Những câu hỏi liên quan
Cho các phản ứng sau: (1) FeS + X1 → X2↑ + X3 (2) X2 + CuSO4 → X4 ↓ (đen) + X5 (3) X2 + X6 → X7↓ (vàng) + X8 (4) X3 + X9 → X10 (5) X10 + HI → X3 + X1 + X11 (6) X1 + X12 → X9 + X8 + MnCl2 Các chất X4, X7, X10 và X12 lần lượt là A. CuO, CdS, FeCl2, MnO2 B. CuS, S, FeCl2, KMnO4 C. CuS, CdS, FeCl3, MnO2 D. CuS, S, FeCl3, MnO2
Đọc tiếp
Cho các phản ứng sau:
(1) FeS + X1 → X2↑ + X3
(2) X2 + CuSO4 → X4 ↓ (đen) + X5
(3) X2 + X6 → X7↓ (vàng) + X8
(4) X3 + X9 → X10
(5) X10 + HI → X3 + X1 + X11
(6) X1 + X12 → X9 + X8 + MnCl2
Các chất X4, X7, X10 và X12 lần lượt là
A. CuO, CdS, FeCl2, MnO2
B. CuS, S, FeCl2, KMnO4
C. CuS, CdS, FeCl3, MnO2
D. CuS, S, FeCl3, MnO2
X1: HCl X2: H2S X3: FeCl2
X4: CuS X5: H2SO4 X6: O2
X7: S X8: H2O X9: Cl2
X10: FeCl3 X11:I2 X12: MnO2
Đáp án D
Đúng 0
Bình luận (0)
Cho các phản ứng sau: (1) FeS + X1 → X2↑ + X3 (2) X2 + CuSO4 → X4 ↓ (đen) + X5 (3) X2 + X6 → X7↓ (vàng) + X8 (4) X3 + X9 → X10 (5) X10 + HI → X3 + X1 + X11 (6) X1 + X12 → X9 + X8 + MnCl2 Các chất X4, X7, X10 và X12 lần lượt là A. CuO, CdS, FeCl2, MnO2 B. CuS, S, FeCl2, KMnO4 C. CuS, CdS, FeCl3, MnO2 D. CuS, S, FeCl3, MnO2
Đọc tiếp
Cho các phản ứng sau:
(1) FeS + X1 → X2↑ + X3
(2) X2 + CuSO4 → X4 ↓ (đen) + X5
(3) X2 + X6 → X7↓ (vàng) + X8
(4) X3 + X9 → X10
(5) X10 + HI → X3 + X1 + X11
(6) X1 + X12 → X9 + X8 + MnCl2
Các chất X4, X7, X10 và X12 lần lượt là
A. CuO, CdS, FeCl2, MnO2
B. CuS, S, FeCl2, KMnO4
C. CuS, CdS, FeCl3, MnO2
D. CuS, S, FeCl3, MnO2
Chọn D
X1: HCl X2: H2S
X3: FeCl2 X4: CuS
X5: H2SO4 X6: O2
X7: S X8: H2O
X9: Cl2 X10: FeCl3
X11:I2 X12: MnO2
Đúng 0
Bình luận (0)
Cho các phản ứng sau: (1) FeS + X1 → X2↑ + X3 (2) X2 + CuSO4 → X4 ↓ (đen) + X5 (3) X2 + X6 → X7↓ (vàng) + X8 (4) X3 + X9 → X10 (5) X10 + HI → X3 + X1 + X11 (6) X1 + X12 → X9 + X8 + MnCl2 Các chất X4, X7, X10 và X12 lần lượt là A. CuO, CdS, FeCl2, MnO2 B. CuS, S, FeCl2, KMnO4 C. CuS, CdS, FeCl3, MnO2 D. CuS, S, FeCl3, MnO2
Đọc tiếp
Cho các phản ứng sau:
(1) FeS + X1 → X2↑ + X3
(2) X2 + CuSO4 → X4 ↓ (đen) + X5
(3) X2 + X6 → X7↓ (vàng) + X8
(4) X3 + X9 → X10
(5) X10 + HI → X3 + X1 + X11
(6) X1 + X12 → X9 + X8 + MnCl2
Các chất X4, X7, X10 và X12 lần lượt là
A. CuO, CdS, FeCl2, MnO2
B. CuS, S, FeCl2, KMnO4
C. CuS, CdS, FeCl3, MnO2
D. CuS, S, FeCl3, MnO2
Đáp án D
X1: HCl
X2: H2S
X3: FeCl2
X4: CuS
X5: H2SO4
X6: O2
X7: S
X8: H2O
X9: Cl2
X10: FeCl3
X11:I2
X12: MnO2
Đúng 0
Bình luận (0)
Thu gọn phân thức:
M
x
10
−
x
8
−
x
7
+
x
6
+
x
4
−
x
2...
Đọc tiếp
Thu gọn phân thức: M = x 10 − x 8 − x 7 + x 6 + x 4 − x 2 − x + 1 x 30 + x 24 + x 18 + x 12 + x 6 + 1 .
Cho x ∈ Q và x ≠ 0. Viết x10 dưới dạng: Thương của hai lũy thừa trong đó số bị chia là x12.
15 x 1,25 x 4 trên 0,25 x10 x12
Mai nộp giúp với ạ . Thánh nào làm được em like
Xem thêm câu trả lời
Cho đa thức
p
x
1
+
x
8
+
1
+
x
9
+
1
+
x
10
+
1
+
x...
Đọc tiếp
Cho đa thức p x = 1 + x 8 + 1 + x 9 + 1 + x 10 + 1 + x 11 1 + x 12 . Khai triển và rút gọn ta được đa thức: P x = a 0 + a 1 x + a 2 x 2 + . . . + a 12 x 12 . Tìm hệ số a 8
A. 720
B. 700
C. 715
D. 730
Cho đa thức
p
x
1
+
x
8
+
1
+
x
9
+
1
+
x
10
+
1
+
x...
Đọc tiếp
Cho đa thức p x = 1 + x 8 + 1 + x 9 + 1 + x 10 + 1 + x 11 1 + x 12 . Khai triển và rút gọn ta được đa thức: P x = a 0 + a 1 x + a 2 x 2 + ... + a 12 x 12 . Tìm hệ số a 8
A. 720
B. 700
D. 730
Đáp án C
Phương pháp: Áp dụng công thức khai triển tổng quát: a + b n = ∑ k = 0 n C n k . a n − k . b k . Đối với bài toán này ta áp dụng công thức 1 + x n = ∑ k = 0 n C n k .1 n − k . x k . Sau đó dựa vào khai triền bài toán cho P x = a 0 + a 1 x + a 2 x 2 + ... + a 2 x 12 ta tìm được hệ số a 8 (đi theo x 8 )
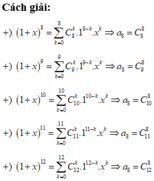
Vậy Hệ số cần tìm là a 8 = C 8 8 + C 9 8 + C 10 8 + C 11 8 + C 12 8 = 1 + 9 + 45 + 165 + 495 = 715
Đúng 0
Bình luận (0)
Cho đa thức
P
x
1
+
x
8
+
1
+
x
9
+
1
+
x
10
+
1
+
x...
Đọc tiếp
Cho đa thức P x = 1 + x 8 + 1 + x 9 + 1 + x 10 + 1 + x 11 + 1 + x 12 . Khai triển và rút gọn ta được đa thức: P x = a 0 + a 1 x + a 2 x 2 + ... + a 12 x 12 . Tìm hệ số a 8 .
A. 700.
B. 730.
C. 720.
D. 715.
Đáp án D
a 8 = C 8 8 + C 9 8 + C 10 8 + C 11 8 + C 12 8 = 1 + 9 + 45 + 165 + 495 = 715
Đúng 0
Bình luận (0)
rút gọn phân thức
1 . 8x3-125 / 3(x-3)-(x-3)(8-4x)
2 . x4-y4 / y3-x3
3 . x10-x8-x7-x6-x5-x4-x3-x2+1 / x30+x24+x18+x12+x6+1
2: \(=\dfrac{\left(x-y\right)\left(x+y\right)\left(x^2+y^2\right)}{-\left(x-y\right)\left(x^2+xy+y^2\right)}=\dfrac{-\left(x+y\right)\left(x^2+y^2\right)}{x^2+xy+y^2}\)
Đúng 1
Bình luận (0)