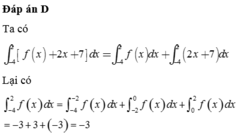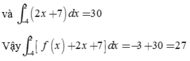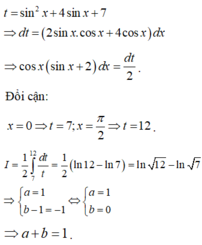Những câu hỏi liên quan
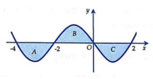
Mỗi hình phẳng A , B, C giởi hạn bởi đồ thị hàm số yf(x)và trục hoành đều có diện tích bằng 3. Tính
∫
−
4
2
f
x
+
2
x
+
7
d
x
A. 35 B. 29. C. 26. D. 27
Đọc tiếp
Mỗi hình phẳng A , B, C giởi hạn bởi đồ thị hàm số y=f(x)và trục hoành đều có diện tích bằng 3. Tính ∫ − 4 2 f x + 2 x + 7 d x
A. 35
B. 29.
C. 26.
D. 27
Đáp án D
Ta có
∫ − 4 2 f x + 2 x + 7 d x = ∫ − 4 2 f x d x + ∫ − 4 2 2 x + 7 d x
Lại có
∫ − 4 2 f x d x = ∫ − 4 − 2 f x d x + ∫ − 2 0 f x d x + ∫ 0 2 f x d x = − 3 + 3 + − 3 = − 3
và ∫ − 4 2 2 x + 7 d x = 30
Vậy ∫ − 4 2 f x + 2 x + 7 d x = − 3 + 30 = 27
Đúng 0
Bình luận (0)
Mỗi hình phẳng A , B, C giởi hạn bởi đồ thị hàm số yf(x) và trục hoành đều có diện tích bằng 3. Tính
∫
−
4
2
f
x
+
2
x
+
7
d
x
A. 35 B. 29 C. 26 D. 27
Đọc tiếp
Mỗi hình phẳng A , B, C giởi hạn bởi đồ thị hàm số y=f(x) và trục hoành đều có diện tích bằng 3. Tính ∫ − 4 2 f x + 2 x + 7 d x
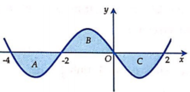
A. 35
B. 29
C. 26
D. 27
Cho \(x_1;x_2;x_3\) là 3 nghiệm của phương trình \(x^3-4x^2+2x+4=0\) thỏa mãn:
\(S_n=x_1^n+x_2^n+x_3^n\) CMR: \(S_n\) là 1 số nguyên
\(\Leftrightarrow\left(x-2\right)\left(x^2-2x-2\right)=0\Rightarrow\left[{}\begin{matrix}x=2\\x^2-2x-2=0\end{matrix}\right.\)
Không mất tính tổng quát, giả sử \(x_3=2\) và \(x_1;x_2\) là nghiệm của \(x^2-2x-2=0\)
Do \(2^n\) nguyên nên ta chỉ cần chứng minh \(P\left(n\right)=x_1^n+x_2^n\) nguyên
\(P\left(1\right)=x_1+x_2=2\in Z\) thỏa mãn
\(P\left(2\right)=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=8\in Z\) thỏa mãn
\(P\left(1\right).P\left(n\right)=\left(x_1+x_2\right)\left(x_1^n+x_2^n\right)=x_1^{n+1}+x_2^{n+1}+x_1x_2\left(x_1^{n-1}+x_2^{n-1}\right)\)
\(\Leftrightarrow2P\left(n\right)=P\left(n+1\right)-2P\left(n-1\right)\)
\(\Leftrightarrow P\left(n+1\right)=2P\left(n\right)+2P\left(n-1\right)\)
\(P\left(1\right);P\left(2\right)\) nguyên \(\Rightarrow P\left(3\right)\) nguyên \(\Rightarrow P\left(4\right)\) nguyên \(\Rightarrow...\Rightarrow P\left(n\right)\) nguyên với mọi n (đpcm)
Đúng 2
Bình luận (1)
Biết
∫
0
1
x
+
2
x
2
+
4
x
+
7
d
x
a
ln
12
+
b
ln
7
, với a, b là các số nguyên. Tổng a + b là : A. -1 B. 1 C....
Đọc tiếp
Biết ∫ 0 1 x + 2 x 2 + 4 x + 7 d x = a ln 12 + b ln 7 , với a, b là các số nguyên. Tổng a + b là :
A. -1
B. 1
C. 0
D. 1 2
Chọn C
∫ 0 1 x + 2 x 2 + 4 x + 7 d x = 1 2 ∫ 0 1 d ( x 2 + 4 x + 7 ) x 2 + 4 x + 7 = 1 2 ln x 2 + 4 x + 7 | 0 1 = 1 2 ln 12 - 1 2 ln 7 = ln 12 - ln 7 = a ln 12 + b ln 7
Do a , b ∈ ℤ ⇒ a = 1 b = - 1 ⇒ a + b = 0
Đúng 0
Bình luận (0)
Biết
∫
0
π
2
sin
x
+
2
cos
x
sin
2
x
+
4
sin
x...
Đọc tiếp
Biết ∫ 0 π 2 sin x + 2 cos x sin 2 x + 4 sin x + 7 d x = a ln 12 + b - 1 ln 7 với a, b là các số nguyên. Tổng a+b bằng:
A. 1.
B. -1.
C. 0.
D. 1 2
Cho phương trình \(x^{2017}+ax^2+bx+c=0\) với các hệ số nguyên có 3 nghiệm \(x_1;x_2;x_3\). CMR nếu \(\left(x_1-x_2\right)\left(x_2-x_3\right)\left(x_3-x_1\right)\)không chia hết có 2017 thì \(a+b+c+1\)chia hết cho 2017
Giả sử \(k_1,k_2,k_3\)là các số nguyên dương; \(k_1+k_2+k_3\)là số lẻ; các số \(x_1,x_2,x_3\)thỏa mãn:
\(\frac{\left|x_1-x_2\right|}{k_1}=\frac{\left|x_2-x_3\right|}{k_2}=\frac{\left|x_3-x_1\right|}{k_3}\)
CMR phương trình sau không có nghiệm nguyên
\(x_1^4+x_2^4+x_3^4+...+x_8^4=2011\)\(x_1^4+x_2^4+...+x_8^4=2011\\ \)
Tìm nghiệm nguyên của phương trình :
\(x_1^4+x_2^4+x_3^4+...+x_8^4=2015\)
nếu tất cả xi chẵn thì xi4 chẵn nên \(x_1^4+x_2^4+x_3^4+...+x_8^4\)chẵn , không thể bằng 2015
nếu có \(x_k\)lẻ \(x_k=2m_k+1,m_k\inℤ,x_k^4=\left(2m_k+1\right)^4=16m_k^3\left(m_k+2\right)+8m_k\left(3m_k+1\right)+1\)
nếu mk chẵn thì \(8m_k\left(3m_k+1\right)⋮16\)
mk lẻ thì \(3m_k+1\)chẵn \(\Rightarrow8m_k\left(3m_k+1\right)⋮16\)
do đó \(x_k^4\)chia cho 16 có số dư là 1
vì vậy \(x_1^4+x_2^4+x_3^4+...+x_8^4\)chia cho 16 có số dư tối đa là 8
còn 2015=125.16+15 khi chia 16 có số dư là 15
vậy không thể xảy ra \(x_1^4+x_2^4+x_3^4+....+x_8^4=2015,x_i\inℤ\)
Với \(x\in Z\)thì: \(x^2\)chia 16 dư 0 hoặc 1. (Tự cm)
\(\Rightarrow x^4=\left(x^2\right)^2:16\)dư 0 hoặc 1
\(\Rightarrow x_1^4+x_2^4+x_3^4+...+x_8^4\)chia 16 sẽ nhận một trong các số dư 0;1;2...;8
Mà \(2015:16\)dư 15\(\Rightarrow\)Phương trình vô nghiệm.