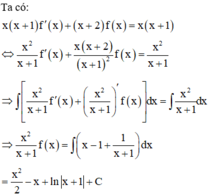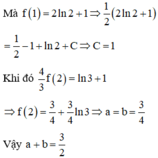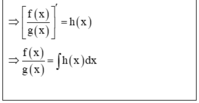Cho a và b là hai số hữu tỉ thỏa mãn ab < 0 và |a| = |b|. Khi đó a phần b = ???

Những câu hỏi liên quan
Cho a và b là hai số hữu tỉ thỏa mãn ab < 0 và |a| = |b|. Khi đó a phần b = ???
Cho a và b là hai số hữu tỉ thỏa mãn ab<0 và giá trị tuyệt đối cua a bằng giá trị tuyệt đối của b khi đó \(\frac{a}{b}\) là
Cho a và b là hai số hữu tỉ thỏa mãn ab<0 và giá trị tuyệt đối cua a bằng giá trị tuyệt đối của b khi đó \(\frac{a}{b}\)là
cho a và b là hai số hửu tỉ thỏa mãn ab<0 và /a/ = /b/ . khi đó a/b = ?
giúp tớ với.
|a|=|b|=> a=-b hoặc a=b (1)
ab<0 => a và b trái dấu (2)
Kết hợp (1) và (2) => a/b=-1
Đúng 0
Bình luận (0)
Cho hàm số
f
x
liên tục trên
ℝ
-
1
;
0
thỏa mãn
x
x
+
1
f
x
+
x
+
2
f
x
x
x...
Đọc tiếp
Cho hàm số f x liên tục trên ℝ \ - 1 ; 0 thỏa mãn x x + 1 f ' x + x + 2 f x = x x + 1 và f 1 = 2 ln 2 + 1 . Khi đó f 2 = a + b ln 3 , với a, b là hai số hữu tỉ. Tính a + b
A. 27 16
B. 15 16
C. 39 16
D. 3 2
Cho a;b;c;d là các số nguyên dương và thỏa mãn: (a/b)<(c/d). tìm một số hữu tỉ x sao cho (a/b)<x<(c/d), từ đó chúng minh rằng ta có thể tìm được các số hữu tỉ khác nhau nằm giữa hai số 1 và 2 (khi biểu diễn trên trục số) mà tổng của chúng lớn hớn 2023 (giải theo trình độ lớp 7)
Cho a, b, c là các số hữu tỉ khác 0 thỏa mãn: a+b+c+d=0. CMR: \(A=\sqrt{\left(ab-cd\right).\left(bc-da\right).\left(ca-bd\right)}\) là số hữu tỉ
Cho a, b, c, d là các số hữu tỉ khác 0 thỏa mãn: a+b+c+d=0. CMR: \(A=\sqrt{\left(ab-cd\right).\left(bc-da\right).\left(ca-bd\right)}\) là số hữu tỉ
Cho a, b, c, d là các số hữu tỉ khác 0 thỏa mãn: a+b+c+d=0. CMR: \(A=\sqrt{\left(ab-cd\right).\left(bc-da\right).\left(ca-bd\right)}\) là số hữu tỉ