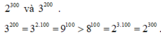2³⁰⁰ = (2³)¹⁰⁰ = 8¹⁰⁰ và 3²⁰⁰ = (3²)¹⁰⁰ = 9¹⁰⁰ nên 2³⁰⁰ < 3²⁰⁰;

Bài 1:

a: Sửa đề: 1/3^200

1/2^300=(1/8)^100

1/3^200=(1/9)^100

mà 1/8>1/9

nên 1/2^300>1/3^200

b: 1/5^199>1/5^200=1/25^100

1/3^300=1/27^100

mà 25^100<27^100

nên 1/5^199>1/3^300

a) \(2^{300}=\left(2^3\right)^{100}=8^{100}\)

\(3^{200}=\left(3^2\right)^{100}=9^{100}>8^{100}\)

\(\Rightarrow2^{300}< 3^{200}\)

b) \(99^{20}=\left(99^2\right)^{10}=9801^{10}< 9999^{10}\Rightarrow99^{20}< 9999^{10}\)

c) \(3^{500}=\left(3^5\right)^{100}=243^{100}\)

\(7^{300}=\left(7^3\right)^{100}=343^{100}>243^{100}\)

\(\Rightarrow3^{500}< 7^{300}\)

Giải chi tiết giúp mình ạ~

\(\left(d\right):202^{303}=\left(202^3\right)^{101}=8242408^{101}>303^{202}=\left(303^2\right)^{101}=91809^{101}\)

\(\left(e\right):107^{50}=\left(107^2\right)^{25}=11449^{25}< 73^{75}=\left(73^3\right)^{25}=389017^{25}\)

A=B

A=B=2³⁰⁰

A=B nhé

\(2^{300}+3^{300}+4^{300}-729.24^{100}=\)

\(=2^{300}+3^{300}+\left(2^2\right)^{300}-3^6.\left(2^3.3\right)^{100}=\)

\(=2^{300}+3^{300}+2^{600}-2^{300}.3^{106}=\)

\(=2^{300}\left(1+2^{300}-3^{106}\right)+3^{300}\)

Ta có

\(2^{300}=\left(2^2\right)^{150}=4^{150}>3^{150}>3^{106}\Rightarrow2^{300}-3^{106}>0\)

\(\Rightarrow2^{300}\left(1+2^{300}-3^{106}\right)+3^{300}>0\)

\(\Rightarrow2^{300}+3^{300}+4^{300}>729.24^{100}\)

Ta có

\(2^{300}+3^{300}+4^{400}=2^{300}+3^{300}+2^{800}.\)

\(729.24^{100}=3^{106}.2^{300}=2^{300}+3^{105}.2^{300}\)

Ta lại có

\(3^{105}+3^{105}+3^{105}+3^{105}.2^{297}=3^{315}+3^{105}.2^{297}\)

Nên chỉ cần so sánh \(3^{105}.2^{297}\)với \(2^{800}\)là đc , dùng logarist cơ số 2 là xong 

Đề bài của mình là 4^300 cơ mà