đầu tiên là gọi ẩn

xong rồi lập phương trình theo những dữ kiện đề bài cho 

và cuối cùng là giải phương trình và lấy nghiệm thỏa mãn điều kiện ban đầu của ẩn

1. Gọi ẩn và đặt điều kiện cho ẩn

2. Lập phương trình theo dữ liệu trong đề bài

3. Giải phương trình và trả lời bài toán

300km

Gọi thời gian của ô tô tả đi từ A->B là: a

Quãng đường A->Blà: AB

Ta có: 2 giờ 30 phút =2,5 giờ.

\(\Leftrightarrow\)\(\begin{cases}40a=AB\\60\left(a-2,5\right)=AB\end{cases}\)\(\Leftrightarrow a=7,5\Rightarrow AB=300\)

Vậy độ dài quãng đường AB là 300 km

Gọi số thứ nhất là x

\(\Rightarrow\)Số thứ hai là 19-x

Theo đề bài ta có phương trình:

x²+(19-x)²=185

\(\Leftrightarrow x^2+361-38x+x^2=185\)

\(\Leftrightarrow2x^2-38x+361-185=0\)

\(\Leftrightarrow2x^2-38x+176=0\)

\(\Leftrightarrow x^2-19x+88=0\)

\(\Leftrightarrow x^2-11x-8x+88=0\)

\(\Leftrightarrow x\left(x-11\right)-8\left(x-11\right)=0\)

\(\Leftrightarrow\left(x-11\right)\left(x-8\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x-11=0\\x-8=0\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}x=11\\x=8\end{cases}}\)

Vậy số thứ nhất là 8, số thứ hai là 19-8=11 hoặc số thứ nhất là 11, số thứ hai là 19-11=8

 Đề : Một hình chữ nhật có chu vi bằng 80 cm. Tăng chiều rộng lên 3cm; tăng chiều dài lên 5 cm thì diện tích tăng thêm 195 cm^2.

Tìm chiều dài và  chiều rộng ban đầu.

a: =>3x=-7/2-1=-9/2

=>x=-3/2

b: =>2(x+4)+3x+2=70

=>2x+8+3x+2=70

=>5x+10=70

hay x=12

c: \(\Leftrightarrow\left(3x-5\right)\left(3x-5-6x-10\right)=0\)

=>(3x-5)(-3x-15)=0

=>x=5/3 hoặc x=-5

d: \(\Leftrightarrow\left(x+1\right)\left(x+2\right)-5\left(x-2\right)=-12+x^2-4\)

\(\Leftrightarrow x^2+3x+2-5x+10=x^2-16\)

=>-2x+12=-16

=>-2x=-28

hay x=14(nhận)

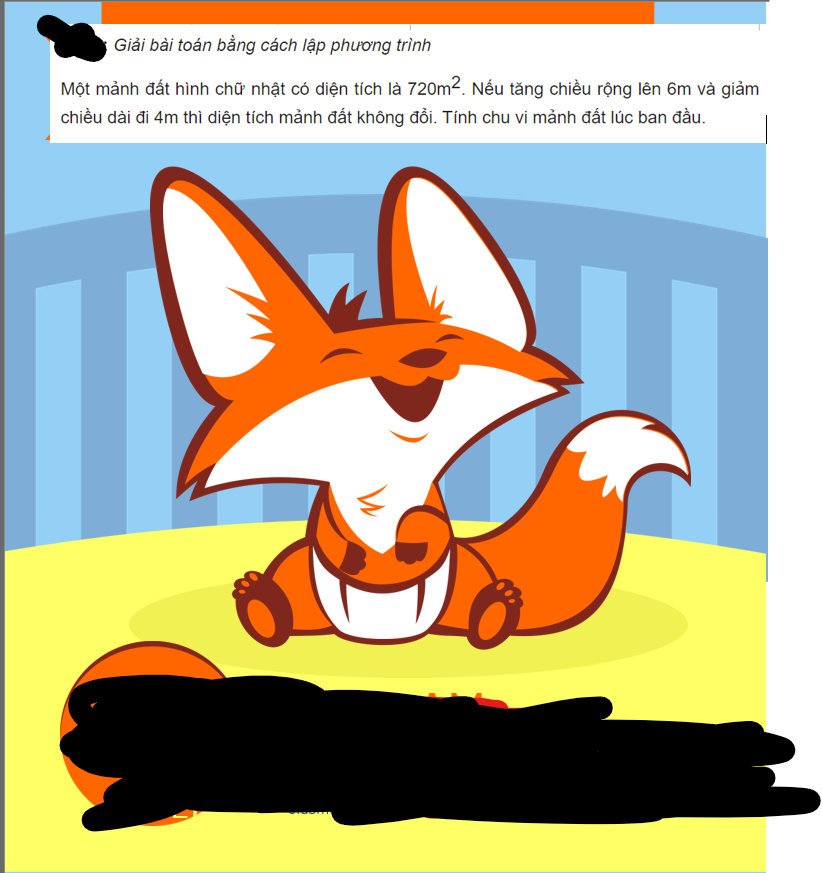
Gọi chiều rộng của mảnh đất hình chữ nhật là \(x\left(m,x>0\right)\)

Chiều dài của mảnh đất hình chữ nhật: \(\dfrac{720}{x}\left(m\right)\)

Chiều rộng mới của mảnh đất hình chữu nhật \(x+6\left(m\right)\)

Chiều dài mới của mảnh đất hình chữ nhật \(\dfrac{720}{x}-4\left(m\right)\)

Theo đề bài, ta có PT: \(\left(x+6\right)\left(\dfrac{720}{x}-4\right)=720\)

\(\Leftrightarrow720-4x+\dfrac{4320}{x}-24=720\)

\(\Leftrightarrow720x-4x^2+4320-24x-720x=0\)

\(\Leftrightarrow-4x^2-24x+4320=0\)

\(\Leftrightarrow\left(x-30\right)\left(x+36\right)=0\)

Vậy \(x=30\)  (thoả mãn)

Chiều rộng của mảnh vườn hình chữ nhật 24m, chiều dài của mảnh vườn hình chữ nhật 30m

Chu vi của mảnh đất hình chữ nhật: \(\left(24+30\right).2=108m\)