Bài 10:Trên cung nhỏ AB của (O), cho hai điểm C và D sao cho cung AB được chia thành 3 cung bằng nhau
Bán kính OC và OD cắt dây AB lần lượt tại E và F.
a) Hãy so sánh các đoạn thẳng AE và FB.
b) Chứng minh các đ thẳng AB và CD song song.
Trên cung nhỏ A B ⏜ của (O), cho hai điểm C và D sao cho cung A B ⏜ được chia thành ba cung bằng nhau ( A C ⏜ = C D ⏜ = D B ⏜ ). Bán kính OC và OD cắt dây AB lần lượt tại E và F
a, Hãy so sánh các đoạn thẳng AE và FB
b, Chứng minh các đường thẳng AB và CD song song
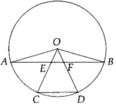
a, Chứng minh được ∆OEA = ∆OFB => AE = FB
b, Chứng minh được O E F ^ = O C D ^ => AB//CD
Trên dây cung AB của một đường tròn O, lấy hai điểm C và D chia dây này thành ba đoạn thẳng bằng nhau AC = CD = DB. Các bán kính qua C và D cắt cung nhỏ AB lần lượt tại E và F. Chứng minh rằng :
a) Cung AE = Cung FB
b) Cung AE = Cung EF
Trên dây cung AB của một đường tròn O,lấy hai điểm C và D chia dây này thành 3 đoạn thẳng bằng nhau AC = CD =DB.Các bán kính qua C và D cắt cung nhỏ AB lần lượt tại E và F
Chứng minh rằng : ∠ AE = ∠ EF
Trên dây cung AB của một đường tròn O,lấy hai điểm C và D chia dây này thành 3 đoạn thẳng bằng nhau AC = CD =DB.Các bán kính qua C và D cắt cung nhỏ AB lần lượt tại E và F
Chứng minh rằng : ∠ AE = ∠ FB
1) Cho (O,R) đường kính AB, vẽ đường tròn tâm O' , đường kính AO. lấy điểm C và D thuộc (O) sao cho B thuộc cung CDvà cung Bc
nhỏ hơn cung BD , các dây AC và AD cắt (O') lần lượt tại E và F
a) So sánh OE và OF
b) So sánh các cung AE và AF của (O')
Trả lời:
a) (O′) có OA là đường kính và E(O′) nên OE⊥AC
Tương tự với (O) ta có BC⊥AC nên OE//BC mà OO là trung điểm của AB
⇒E là trung điểm của AC⇒ OE=12BC.
Tương tự OF=12DB mà cung BC bằng cung BD nên BC=BD⇒OE=OF hay cung OE= cung OF.
~Học tốt!~
1) Cho (O,R) đường kính AB, vẽ đường tròn tâm O' , đường kính AO. lấy điểm C và D thuộc (O) sao cho B thuộc cung CDvà cung Bc nhỏ hơn cung BD , các dây AC và AD cắt (O') lần lượt tại E và F
a) So sánh OE và OF
b) So sánh các cung AE và AF của (O')
trên cung nhỏ AB của (O), lấy hai điểm E,F sao cho sđAE = sđ EF= sđ FB, dây AB lần lượt cắt các bán kính OE và OF tại C và D. CMR: AB>3CD
Cho đường tròn (O) và dây AB không là đường kính, C là một điểm trên AB, D là 1 điểm trên cung nhỏ AB của (O), OD cắt AB tại E. đường thẳng OC cắt \(\left(O^,\right)\)ngoại tiếp tam giác OAB tại F, EF cắt \(\left(O^,\right)\)tại G, GD cắt\(\left(O^,\right)\)tại H. Chứng minh:
1) tam giác OCD đồng dạng tam giác ODF từ đó suy ra góc CFD= góc CDO
2)Gọi S là trung điểm của CD. Chứng minh 3 điểm O,H,S thẳng hàng
Cho đường tròn (O) có dây AB khác đường kính. Điểm C bất kì trên AB và D bất kì trên cung nhỏ AB. Tia OC cắt đường tròn (OAB) tại F khác O. Đoạn OD cắt AB tại E. Đường thẳng FE cắt (OAB) tại G khác F. Tia GD cắt lại (OAB) ở Q. Chứng minh OQ chia đôi CD ?
Gọi R đối xứng với D qua O. Khi đó DR là đường kính của (O) hay O là trung điểm RD.
Ta có: ^OBC = ^BFO (2 góc nội tiếp chắn (OA=(OB ) nên \(\Delta\)OCB ~ \(\Delta\)OBF (g,g)
Suy ra: OB2 = OC.OF hay OR2 = OC.OF. Từ đó: \(\Delta\)OCR ~ \(\Delta\)ORF (c.g.c) => ^ORC = ^OFR
Áp dụng hệ thức lượng đường tròn có: EG.EF = EA.EB = ED.ER nên tứ giác GDFR nội tiếp
Suy ra: ^OFR = ^GFR - ^GFO = ^GDR - ^GQO = ^DOQ. Từ đấy: ^ORC = ^DOQ
Do đó: CR // OQ. Xét trong \(\Delta\)DRC thấy: O trung điểm RD và OQ // CR cho nên OQ đi qua trung điểm CD (đpcm).