Các câu hỏi tương tự
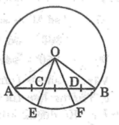
Trên dây cung AB của một đường tròn O,lấy hai điểm C và D chia dây này thành 3 đoạn thẳng bằng nhau AC = CD =DB.Các bán kính qua C và D cắt cung nhỏ AB lần lượt tại E và F
Chứng minh rằng : ∠ AE = ∠ EF
Trên cung nhỏ
A
B
⏜
của (O), cho hai điểm C và D sao cho cung
A
B
⏜
được chia thành ba cung bằng nhau (
A
C
⏜
C
D
⏜
D...
Đọc tiếp
Trên cung nhỏ A B ⏜ của (O), cho hai điểm C và D sao cho cung A B ⏜ được chia thành ba cung bằng nhau ( A C ⏜ = C D ⏜ = D B ⏜ ). Bán kính OC và OD cắt dây AB lần lượt tại E và F
a, Hãy so sánh các đoạn thẳng AE và FB
b, Chứng minh các đường thẳng AB và CD song song
Bài 10:Trên cung nhỏ AB của (O), cho hai điểm C và D sao cho cung AB được chia thành 3 cung bằng nhau
Bán kính OC và OD cắt dây AB lần lượt tại E và F.
a) Hãy so sánh các đoạn thẳng AE và FB.
b) Chứng minh các đ thẳng AB và CD song song.
Cho đường tròn (O), dây AB cố định không đi qua O; Lấy hai điểm C và D thuộc
dây AB sao cho AC = CD = DB. Các bán kính qua C và D cắt cung nhỏ AB tại E và
F.
a) Chứng minh AE < EF
b) Một điểm M di động trên đường tròn (O), điểm P thuộc đoạn thẳng AM, điểm Q
thuộc đoạn thẳng BM sao cho AP = BQ. Chứng minh đường trung trực của PQ luôn
đi qua điểm cố định.
Cho đường tròn tâm (O) và dây AB, lấy 2 điểm M,N nằm trên cung nhỏ AB chia cung này thành 3 cung bang nhau là Cung AM=Cung MN=Cung NB. Các bán kính OM và ON cắt AB tại C và D. Chứng minh rằng:
a. AC=BD
b. AC > CD
Cho đường tròn tâm (O) và dây AB, lấy 2 điểm M,N nằm trên cung nhỏ AB chia cung này thành 3 cung bang nhau là Cung AM=Cung MN=Cung NB. Các bán kính OM và ON cắt AB tại C và D. Chứng minh rằng:
a. AC=BD
b. AC > CD
Cho đường tròn tâm (O) và dây AB, lấy 2 điểm M,N nằm trên cung nhỏ AB chia cung này thành 3 cung bang nhau là Cung AM=Cung MN=Cung NB. Các bán kính OM và ON cắt AB tại C và D. Chứng minh rằng:
a. AC=BD
b. AC > CD
trên cung nhỏ AB của (O), lấy hai điểm E,F sao cho sđAE = sđ EF= sđ FB, dây AB lần lượt cắt các bán kính OE và OF tại C và D. CMR: AB>3CD
Bài 4 Cho nửa đường tròn đường kính AB và dây AC. Từ một điểm D trên AC, vẽ DE vuông góc với AB. Hai đường thẳng DE và BC cắt nhau tại F. Chứng minh rằng:a) Tứ giác BCDE nội tiếp.b)góc AFE ACE.Bài 5. Cho nứa đường tròn đường kính AB. Lấy hai điểm C và D trên nửa đường tròn sao cho cung AC cung CD cung DB. Các tiếp tuyến vẽ từ B và C của nửa đường tròn cắt nhau tại I.Hai tia AC và BD cắt nhau tại K. Chứng minh rằng:a) Các tam giác KAB và IBC là những tam giác đêu.b) Tứ giác KIBC nội tiếp.Bài 6. C...
Đọc tiếp
Bài 4 Cho nửa đường tròn đường kính AB và dây AC. Từ một điểm D trên AC, vẽ DE vuông góc với AB. Hai đường thẳng DE và BC cắt nhau tại F. Chứng minh rằng:
a) Tứ giác BCDE nội tiếp.
b)góc AFE= ACE.
Bài 5. Cho nứa đường tròn đường kính AB. Lấy hai điểm C và D trên nửa đường tròn sao cho cung AC= cung CD= cung DB. Các tiếp tuyến vẽ từ B và C của nửa đường tròn cắt nhau tại I.Hai tia AC và BD cắt nhau tại K. Chứng minh rằng:
a) Các tam giác KAB và IBC là những tam giác đêu.
b) Tứ giác KIBC nội tiếp.
Bài 6. Cho nửa đường tròn (0) đường kính AB và tia tiếp tuyến Bx của nửa đường tròn. Trên tia Bx lấy hai điểm C và D (C nằm giữa B và D). Các tia AC và BD lần lượt cắt đường tròn tại E và F. Hai dây AE và BF cắt nhau tại M. Hai tia AF và BE cắt nhau tại N. Chứng minh rằng:
a) Tứ giác FNEM nội tiêp.
b) Tứ giác CDFE nội tiếp.
Bài 7. Cho tam giác ABC. Hai đường cao BE và CF cắt nhau tại H. Gọi D là điểm đối xứng của H qua trung điểm M của BC.
a) Chứng minh rằng tứ giác ABDC nội tiếp được đường tròn. Xác định tâm 0 của đường tròn đó
b) Đường thẳng DH cắt đường tròn (0) tại điểm thứ hai là I. Chứng minh rằng năm điểm A, I, F, H, E cùng nằm trên một đường tròn
Các bạn giải giúp mình các bài này nhé, mình cảm ơn nhiều lắm