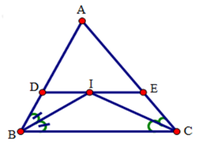
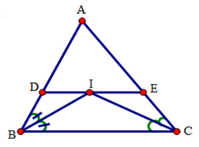
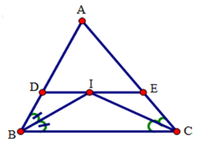
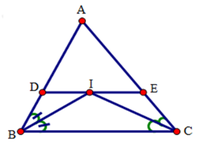
1. Cho tam giác abc. Các tia phân giác của các góc b và c cắt nhau tại i. Qua i kẻ đường thẳng song song vói ab, cắt ac và bc ở d và e. CMR: de = ad + be
2. Cho tam giác abc vuông tại a. Các tia phân giác của các góc b và c cát nhau tại i. Kẻ ih vuông góc với bc(h thuộc bc). Biết hi = a; hb = 2a; hc = 3a. Tính chu vi tam giác abc.
3. Tm giác abc có i là giao điểm các tia phân giác của các góc b và c. Gọi d là giao điểm của ai và bc. Kẻ ih vuông góc với bc(h thuộc bc). CMR: góc bih = góc cid.
4.Cho tam giác abc có góc b> góc c, đường phân giác ad. Gọi h là chân đường vuông góc kẻ từ a đến bc. CMR: góc had=góc(b-c)/2.
5. Tam giác abc có góc b lớn hơn góc c 90 độ. Các đường phân giác trong và ngoài của góc a cắt bc ở d và e. CMR:tam giác ade vuông cân.
6. Cho tam giác abc, ad là phân giác trong của góc a. CMR: bd/dc = ab/ac.
7. Cho tam giác abc, bc = a, ca = b, ab = c. Các phân giác ad, be, cf cắt nhau tại i. CMR:a) di/da = a/a+b+c
b) di/da + ei/eb + fi/fc = 1