Xét tam giác ABC vuông tại A:

BI; IC là đường phân giác (gt).

BI cắt CI tại I (gt).

\(\Rightarrow\) AI là tia phân giác góc BAC.

Tam giác ABC có BI; CI là các đường phân giác giao nhau tại I

=> I là tâm đường tròn ngoại tiếp

=> AI là phân giác

Xét tam giác ABC vuông tại A:

BI; IC là đường phân giác (gt).

BI cắt CI tại I (gt).

 AI là tia phân giác góc BAC.

vẽ hình nữa nha

Kẻ IK,IH,IE lần lượt vuông góc BC,AB,AC

Xét ΔBHI vuông tại H và ΔBKI vuông tại K có

BI chung

góc HBI=góc KBI

=>ΔBHI=ΔBKI

=>IH=IK

Xét ΔCKI vuông tại K và ΔCEI vuông tại E có

CI chung

góc KCI=góc ECI

=>ΔCKI=ΔCEI

=>IK=IE

=>IH=IE

Xét ΔAHI vuông tại H và ΔAEI vuông tại E có

AI chung

IH=IE

=>ΔAHI=ΔAEI

=>góc HAI=góc EAI

=>AI là phân giác của góc BAC

XétΔABC có

BI,CI là các tia phân giác

BI cắt CI tại I

Do đó: I là tâm đường tròn nội tiếp

hay AI là tia phân giác của góc BAC

moi hok lop 6

Sửa đề: Phân giác góc B,C cắt nhau tại I

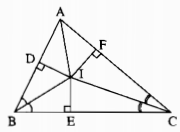
Kẻ ID⊥AB tại D, IF⊥AC tại F, IE⊥BC tại E

Xét ΔIDB vuông tại D và ΔIEB vuông tại E có 

IB chung

\(\widehat{DBI}=\widehat{EBI}\)(BI là tia phân giác của \(\widehat{DBE}\))

Do đó: ΔIDB=ΔIEB(cạnh huyền-góc nhọn)

⇔ID=IE(hai cạnh tương ứng)(1)

Xét ΔIEC vuông tại E và ΔIFC vuông tại F có

IC chung

\(\widehat{ECI}=\widehat{FCI}\)(CI là tia phân giác của \(\widehat{ECF}\))

Do đó: ΔIEC=ΔIFC(cạnh huyền-góc nhọn)

⇒IE=IF(hai cạnh tương ứng)(2)

Từ (1) và (2) suy ra ID=IF(=IE)

Xét ΔADI vuông tại D và ΔAFI vuông tại F có

AI chung

ID=IF(cmt)

Do đó: ΔADI=ΔAFI(cạnh huyền-cạnh góc vuông)

⇒\(\widehat{DAI}=\widehat{FAI}\)(hai góc tương ứng)

⇒\(\widehat{BAI}=\widehat{CAI}\)

mà tia AI nằm giữa hai tia AB,AC

nên AI là tia phân giác của \(\widehat{BAC}\)(đpcm)

Xét ΔABC có

BI là phân giác

CI là phân giác

BI cắt CI tại I

Do đó: I là tâm đường tròn nội tiếp ΔABC

=>AI là tia phân giác của góc BAC

1.Vì các tia phân giác của các góc B và C cắt nhau tại I

\(\Rightarrow\)I là giao của các đường phân giác trong tam giác

\(\Rightarrow\)AI là tia phân giác của góc A

1.

Kẻ: \(ID\perp AB;IE\perp BC;IF\perp AC\)

\(\widehat{IDB}=\widehat{IEB}=90^0\)

\(\widehat{DBI}=\widehat{EIB}\left(gt\right)\)

BI cạnh huyền chung

⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)

Suy ra: ID = IE (hai cạnh tương ứng)       (1)

Xét hai tam giác vuông IEC và IFC, ta có ;

\(\widehat{IEC}=\widehat{IFC}=90^0\)

\(\widehat{ECI}=\widehat{FCI}\left(gt\right)\)

CI canh huyền chung

Suy ra:  ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)

Suy ra: IE = IF (hai cạnh tương ứng)           (2)

Từ (1) và (2) suy ra: ID = IF

Xét hai tam giác vuông IDA và IFA, ta có:

         \(\widehat{IDA}=\widehat{IFA}=90^0\)

            ID = IF (chứng minh trên)

            AI cạnh huyền chung

Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)

Suy ra\(\widehat{DAI}=\widehat{FAI}\) (hai góc tương ứng)

Vậy AI là tia phân giác của \(\widehat{A}\)

2. Cho tam giác ABC có AB < AC. Tia phân giác của góc A cắt đường trung trực của BC tại I. Kẻ IH vuông góc với đường thẳng AB, kẻ IK vuông góc với đường thẳng AC. Chứng minh rằng BH = CK. 

Xét ∆BMI và ∆CMI, ta có:

+) BM = CM (vì IM là đường trung trực của BC)

+)\(\widehat{BMI}=\widehat{CMI}=90^0\)

+) MI cạnh chung 

Suy ra: ∆BMI = ∆CMI (c.g.c)

⇒ IB = IC (hai cạnh tương ứng)

Xét hai tam giác vuông IHA và IKA, có: 

+) \(\widehat{HAI}=\widehat{KAI}\) (AI là phân giác góc A)

+) AI cạnh huyền chung

Suy ra: ∆IHA = ∆IKA (cạnh huyền - góc nhọn)

Suy ra: IH = IK (hai cạnh tương ứng)

Xét hai tam giác vuông IHB và IKC, có:

+) IB = IC (chứng minh trên)

+) IH = IK (chứng minh trên)

Suy ra: ∆IHB = ∆IKC (cạnh huyền - cạnh góc vuông)

Suy ra: BH = CK (2 cạnh tương ứng)