Làm giùm em câu 29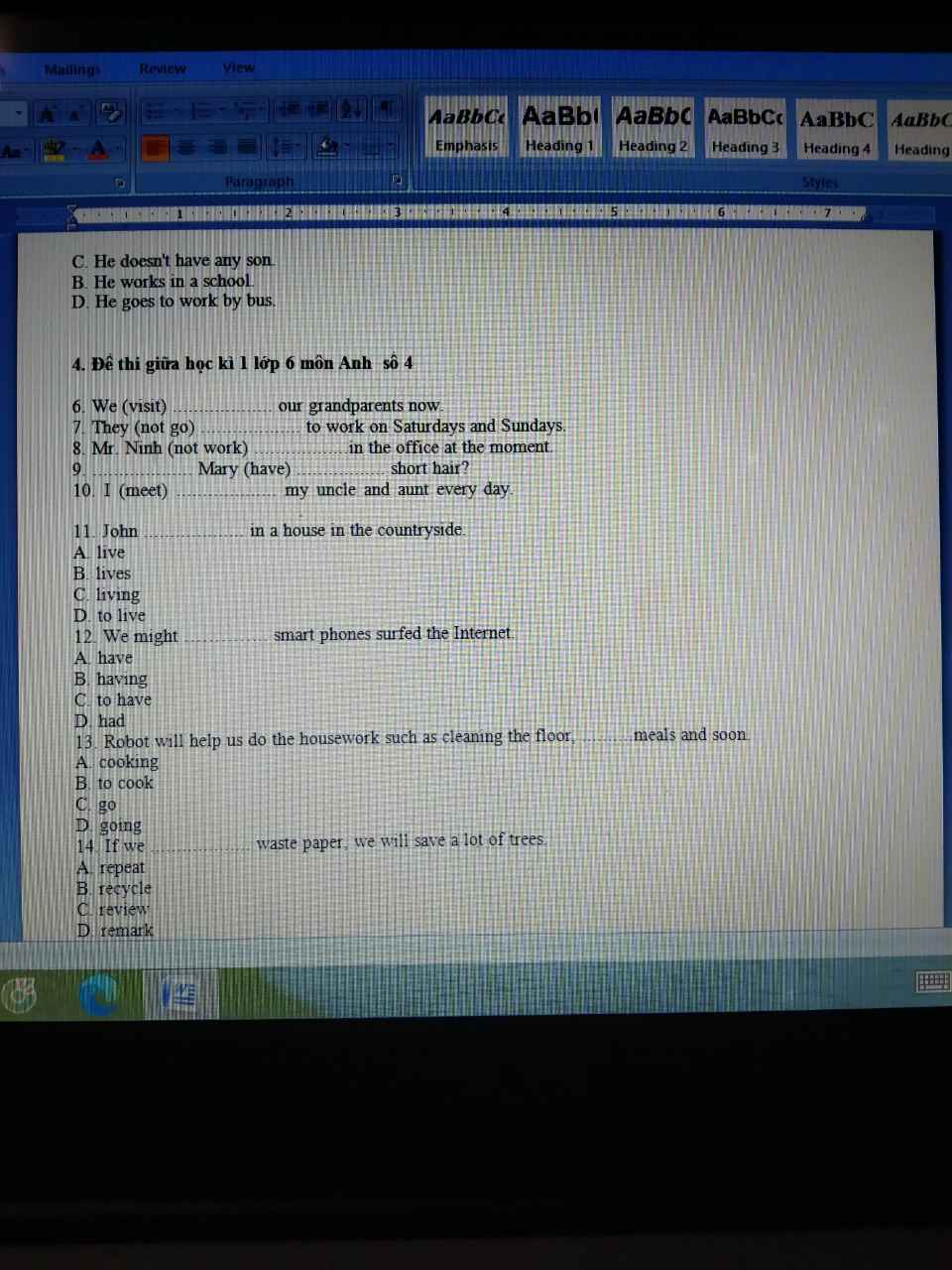

Những câu hỏi liên quan
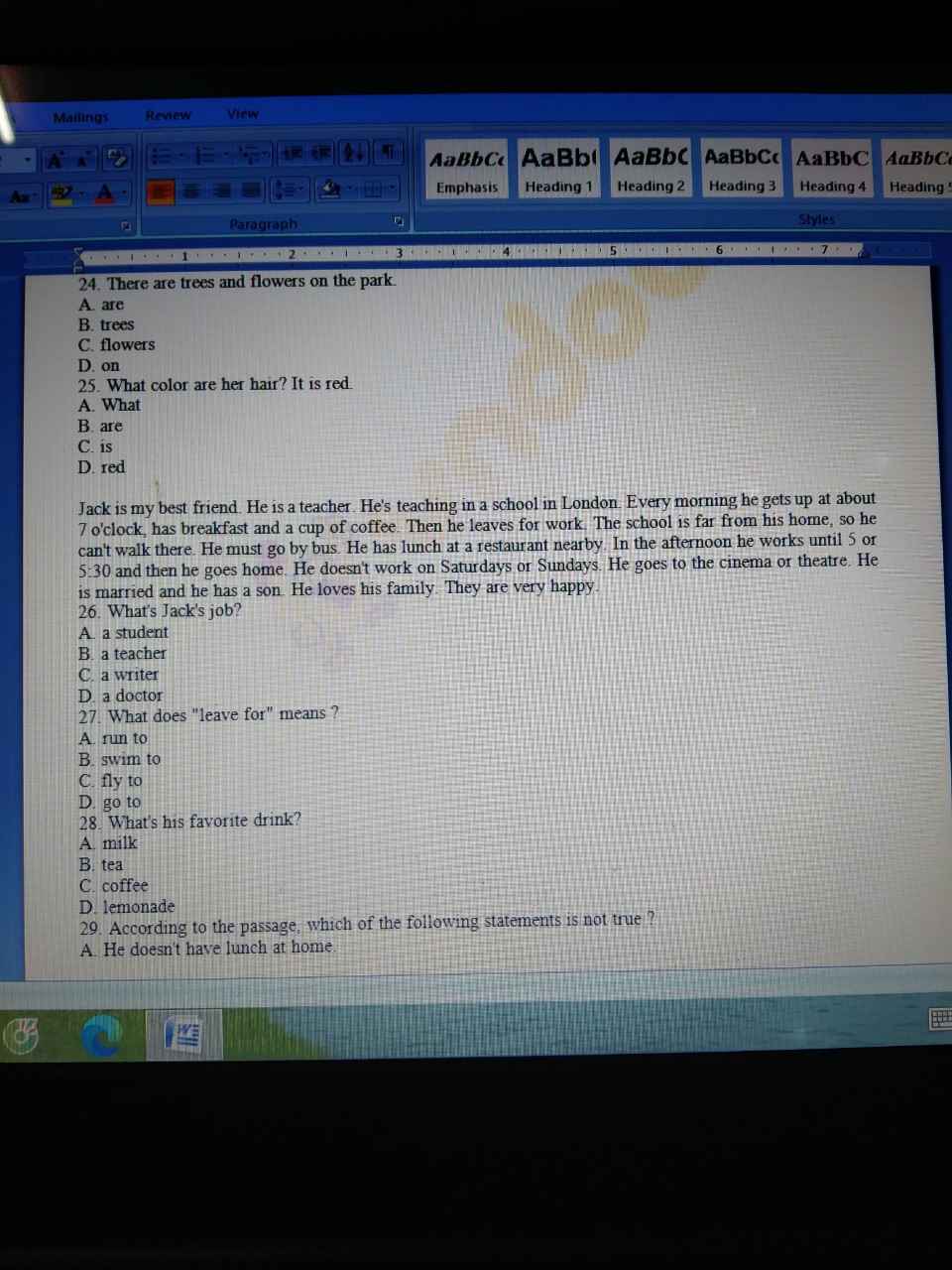
Làm giùm em câu 4
Bài 4:
1) Ta có: \(a\left(b+n\right)=ab+an\)(1)
\(b\left(a+n\right)=ab+bn\)(2)
Nếu a<b thì an<bn
hay \(ab+an< ab+bn\)(3)
Từ (1), (2) và (3) suy ra \(\dfrac{a}{b}< \dfrac{a+n}{b+n}\)
Nếu a>b thì an>bn
hay an+ab>bn+ab(4)
Từ (1), (2) và (4) suy ra \(\dfrac{a}{b}>\dfrac{a+n}{b+n}\)
Nếu a=b thì an=bn
hay an+ab=bn+ab(5)
Từ (1), (2) và (5) suy ra \(\dfrac{a}{b}=\dfrac{a+n}{b+n}\)
Đúng 0
Bình luận (0)
Bài 1:
a) Đúng
b) Đúng
c) Sai
d) Sai
e) Sai
Đúng 0
Bình luận (0)
Giải giùm em với biết câu nào làm câu đó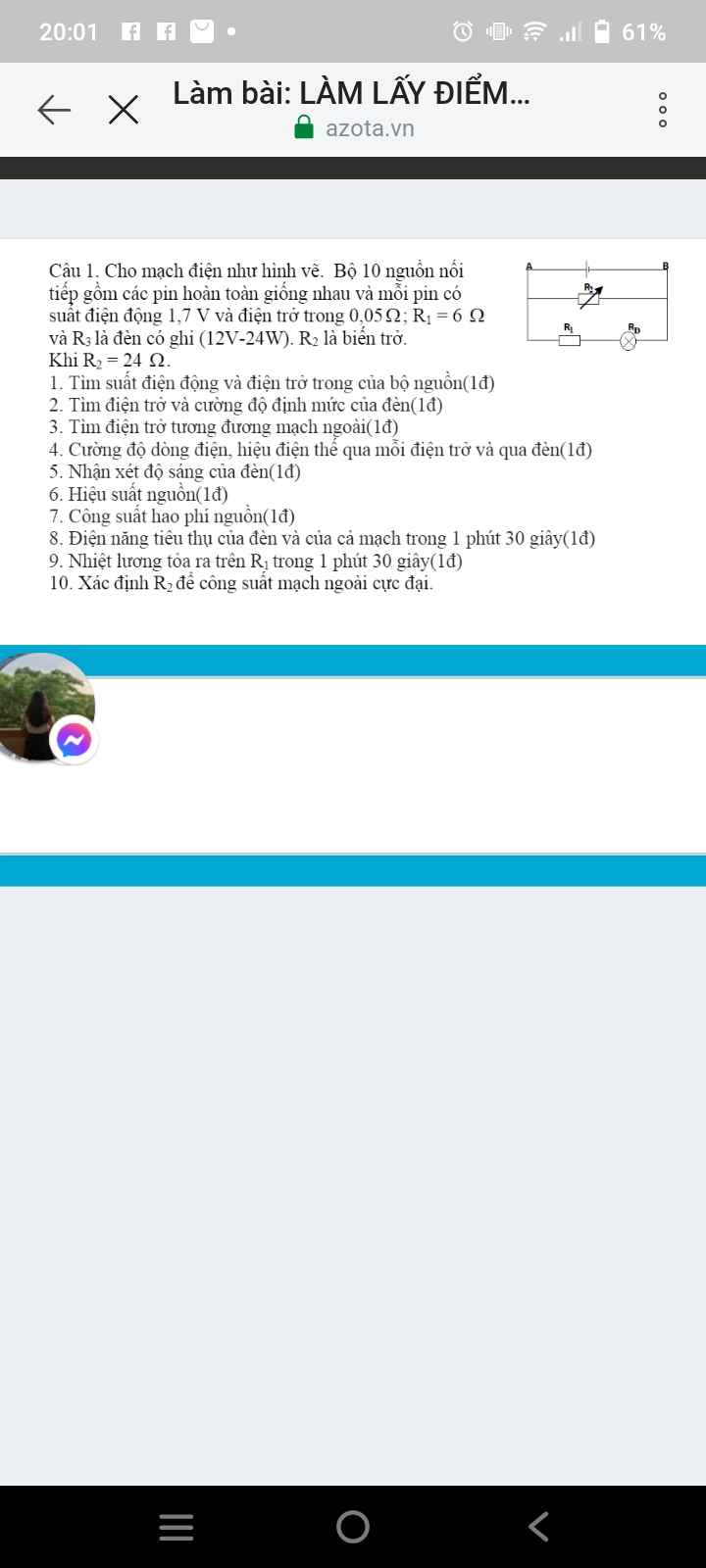
Làm giùm em câu 3 với 
3)
a/ -5 bé hơn \(\dfrac{1}{63}\)
b)\(\dfrac{-18}{17}\)bé hơn \(\dfrac{-999}{1000}\)
c) \(\dfrac{-17}{35}\)lơn hơn \(\dfrac{-43}{85}\)
d) \(\dfrac{-13}{38}\)bé hơn\(\dfrac{29}{-88}\)
e)-0,76 bé hơn \(\dfrac{-19}{28}\)
f) \(\dfrac{-18}{31}=\dfrac{-181818}{313131}\)
Đúng 3
Bình luận (1)
Làm giùm em câu 15 với 
Câu 15:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{5}=\dfrac{b}{4}=\dfrac{c}{6}=\dfrac{a+b-c}{5+4-6}=\dfrac{90}{3}=30\)
Do đó: a=150; b=120; c=180
Đúng 0
Bình luận (0)
Làm giùm em câu 15 với
gọi số sách ủng hộ của 3 lớp lần lượt là a,b,c(a,b,c>0)
theo bài ra ,ta có
a/4=b/5=c/6 và a+b-c=90
áp dụng tính chất dãy tỉ số bằng nhau
a/4=b/5=c/6=a+b-c/4+5-6=90/3=30
vậy 8A=30.4=120
8B=30.5=150
8C=30.6=180
Đúng 0
Bình luận (0)
Làm giùm em câu 3 với
Làm giùm em câu 11,12 với
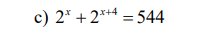 làm giùm em câu này với
làm giùm em câu này với
\(\Rightarrow2^x\left(1+2^4\right)=544\\ \Rightarrow2^x\cdot17=544\\ \Rightarrow2^x=32=2^5\\ \Rightarrow x=5\)
Đúng 0
Bình luận (0)
Dạ nhờ anh chị giải giùm em 2 câu này, câu 61 em làm sợ sai nên gửi lên nhờ anh chị giải để em xem làm có đúng không thôi ạ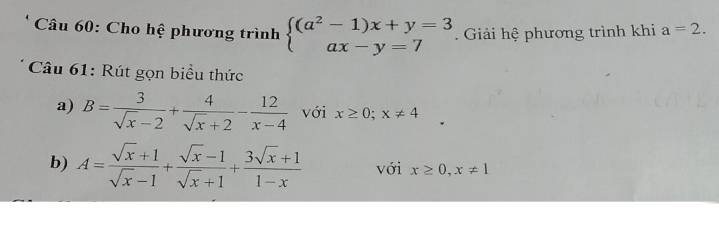
Câu 61:
a: \(B=\dfrac{3}{\sqrt{x}-2}+\dfrac{4}{\sqrt{x}+2}-\dfrac{12}{x-4}\)
\(=\dfrac{3}{\sqrt{x}-2}+\dfrac{4}{\sqrt{x}+2}-\dfrac{12}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{3\left(\sqrt{x}+2\right)+4\left(\sqrt{x}-2\right)-12}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3\sqrt{x}+6+4\sqrt{x}-8-12}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{7\sqrt{x}-14}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{7\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{7}{\sqrt{x}+2}\)
b: \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}+\dfrac{\sqrt{x}-1}{\sqrt{x}+1}+\dfrac{3\sqrt{x}+1}{1-x}\)
\(=\dfrac{\left(\sqrt{x}+1\right)}{\sqrt{x}-1}+\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}+1\right)^2+\left(\sqrt{x}-1\right)^2-3\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x+2\sqrt{x}+1+x-2\sqrt{x}+1-3\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{2x-3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(2\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\)
Câu 60
Khi a=2 thì hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}\left(2^2-1\right)x+y=3\\2x-y=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x+y=3\\2x-y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x=10\\2x-y=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2\\y=2x-7=2\cdot2-7=-3\end{matrix}\right.\)
Đúng 2
Bình luận (1)

















