x3 - 5x2 + 7x - 3 / x2 - 1 khi x khác 1
2m + 1 khi x =1 liên tục tại x0 = 1
Những câu hỏi liên quan
Giá trị của tham số m để hàm số
y
x
3
-
1
x
-
1
k
h
i
...
Đọc tiếp
Giá trị của tham số m để hàm số y = x 3 - 1 x - 1 k h i x ≠ 1 2 m + 1 k h i x = 1 liên tục tại x 0 = 1 là
A. m = 2
B. m = 1
C. m = 0
D. m = - 1 2
Cho hàm số
f
(
x
)
x
3
-
1
x
-
1...
Đọc tiếp
Cho hàm số f ( x ) = x 3 - 1 x - 1 k h i x ≠ 1 2 m + 1 k h i x = 1 . Giá trị của tham số m để hàm số liên tục tại điểm x0 = 1 là:
A. m = 1
B. m = - 1 2
C. m = 0
D. m = 2
Đáp án A.
Phương pháp: Hàm số y = f(x) liên tục tại 
Cách giải: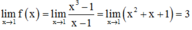 
f(1) = 2m+1
Để hàm số liên tục tại x = 1
Đúng 0
Bình luận (0)
Cho hàm số
y
f
x
2
x
2
−
7
x
+
6
x...
Đọc tiếp
Cho hàm số y = f x = 2 x 2 − 7 x + 6 x − 2 k h i x < 2 a + 1 − x 2 + x k h i x ≥ 2 . Biết a là giá trị để hàm số f(x) liên tục tại x 0 = 2 , tìm nghiệm nguyên của bất phương trình − x 2 + a x + 7 4 > 0 .
A. 1
B. 4
C. 3
D. 2
Đáp án D
Ta có lim x → 2 − f x = lim x → 2 − 2 x 2 − 7 x + 6 x − 2 = lim x → 2 − 2 x 2 − 7 x + 6 x − 2 = lim x → 2 − − 2 x − 3 = − 1
Và lim x → 2 − f x = lim x → 2 − a + 1 − x 2 + x = a − 1 4 ; f 2 = a − 1 4 .
Theo bài ra, ta có lim x → 2 + f x = lim x → 2 − f x = f 2 ⇒ a = − 3 4
Do đó, bất phương trình − x 2 + a x + 7 4 > 0 ⇔ − x 2 − 3 4 x + 7 4 > 0 ⇔ − 7 4 < x < 1.
Đúng 0
Bình luận (0)
Hàm số
f
x
x
2
−
1
khi
x
≤
1
x
+
m
khi
x...
Đọc tiếp
Hàm số f x = x 2 − 1 khi x ≤ 1 x + m khi x > 1 liên tục tại điểm x 0 = 1 khi m nhận giá trị
A. m = 1
B. m = 2
C. m bất kì
D. m = − 1
Đáp án D
Ta có lim x → 1 + f x = lim x → 1 + x 2 − 1 = 0 , lim x → 1 − f x = lim x → 1 − x + m = 1 + m , f 1 = 1 2 − 1 = 0
để hàm số liên tục tại x 0 = 1 thì lim x → 1 + f x = lim x → 1 − f x = f 1 ⇔ 0 = 1 + m ⇔ m = − 1
Đúng 0
Bình luận (0)
Hàm số
f
x
x
2
+
1
khi x
≤
1
x
+
m
khi x
1...
Đọc tiếp
Hàm số f x = x 2 + 1 khi x ≤ 1 x + m khi x > 1 liên tục tại điểm x 0 = 1 khi m nhận giá trị
A. m=-2
B. m=2
C. m=-1
D. m=1
Đáp án D
Ta có
lim x → 1 + f x = lim x → 1 + x + m = 1 + m lim x → 1 − f x = lim x → 1 − x 2 + 1 = 2 f 1 = 2
Hàm số liên tục tại diểm x 0 = 1 ⇔ lim x → 1 + f x = lim x → 1 − f x = f 1 ⇒ 1 + m = 2 ⇔ m = 1
Đúng 0
Bình luận (0)
Cho hàm số
f
(
x
)
-
x
3
-
6
x
2...
Đọc tiếp
Cho hàm số f ( x ) = - x 3 - 6 x 2 + x + 6 x - 1 k h i ≠ 1 2 m + 4 k h i x = 1 . Tìm giá trị của m để hàm số liên tục tại x=1.
A.5
B. -18
C. -9
D.14
Đáp án C
Ghi nhớ: Cho hàm số 
xác định trên khoảng 
và 
. Hàm số 
liên tục tại 
khi 
Đúng 0
Bình luận (0)
Hàm số
f
(
x
)
x
2
-
1
k
h
i
x
⩽
1
x
+...
Đọc tiếp
Hàm số f ( x ) = x 2 - 1 k h i x ⩽ 1 x + m k h i x > 1 liên tục tại điểm x 0 = 1 khi m nhận giá trị bằng bao nhiêu?
A. m=1.
B. m=2.
C. m ∈ ∅ .
D. m=-1.
Tìm a để hàm số
f
(
x
)
x
2
-
1
x
-...
Đọc tiếp
Tìm a để hàm số f ( x ) = x 2 - 1 x - 1 k h i x ≠ 1 a k h i x = 1 liên tục tại điểm x0=1.
A. 
.
B. 
.
C. 
.
D. 
.
Chọn C
TXĐ: 
.
Ta có : 
.
.
Hàm số 
liên tục tại điểm 
khi và chỉ khi 
.
Đúng 0
Bình luận (0)
Cho hàm số
f
x
x
3
-
1
x
-
1
k
h
i
x...
Đọc tiếp
Cho hàm số f x = x 3 - 1 x - 1 k h i x ≠ 1 2 m + 1 k h i x = 1 . Giá trị của tham số m để hàm số liên tục tại điểm x ∘ = 1 là:
A. m = 2
B. m = 1 .
C. m = 0
D. m = - 1 2
