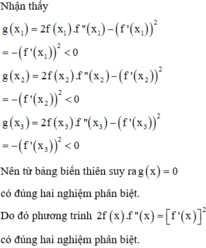có bao nhiêu cặp (a,b) để phương trình sau có nghiệm x∈R : (x-1)(x+2)(ax2+bx+2)≥0

Những câu hỏi liên quan
Cho hàm số
f
(
x
)
x
3
+
a
x
2
+
b
x
+
c
. Nếu phương trình
f
(
x
)
0
có ba nghiệm phân biệt thì phương trình
2
f
(
x
)
.
f
”
(
x
)...
Đọc tiếp
Cho hàm số f ( x ) = x 3 + a x 2 + b x + c . Nếu phương trình f ( x ) = 0 có ba nghiệm phân biệt thì phương trình 2 f ( x ) . f ” ( x ) = [ f ’ ( x ) ] 2 có nhiều nhất bao nhiêu nghiệm?
A. 1 nghiệm
B. 4 nghiệm
C. 3 nghiệm
D. 2 nghiệm
Cho hàm số
f
x
x
3
+
a
x
2
+
b
x
+
c
.
Nếu phương trình
f
x
0
có ba nghiệm phân biệt thì phương trình
2
f
x
.
f
x
f...
Đọc tiếp
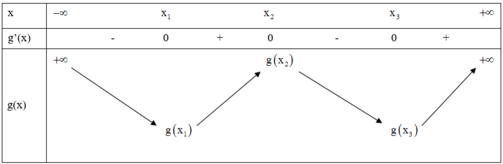
Cho hàm số f x = x 3 + a x 2 + b x + c . Nếu phương trình f x = 0 có ba nghiệm phân biệt thì phương trình 2 f x . f ' ' x = f ' x 2 có bao nhiêu nghiệm.
A. 3
B. 1
C. 2
D. 4
Đáp án C
Cho a = 0 , b = − 3 , c = 0 ⇒ f x = x 3 − 3 x 2 = 0 có 3 nghiệm phân biệt.
Ta có:
f ' x = 3 x 2 − 6 x f ' ' x = 6 x − 6 ⇒ 2 x 3 − 3 x 2 6 x − 6 = 3 x 2 − 6 x 2 ⇔ 12 x 2 x − 3 x − 1 = 9 x 2 x − 2 2 ⇔ x = 0 4 x 2 − 4 x + 3 = 3 x 2 − 4 x + 4 ⇔ x = 0 x = 4
Đúng 0
Bình luận (0)
Chứng tỏ rằng nếu phương trình
a
x
2
+
b
x
+
c
0
có nghiệm là
x
1
v
à
x
2
thì tam thức
a
x
2
+
b
x
+...
Đọc tiếp
Chứng tỏ rằng nếu phương trình a x 2 + b x + c = 0 có nghiệm là x 1 v à x 2 thì tam thức a x 2 + b x + c phân tích được thành nhân tử như sau:
a x 2 + b x + c = a ( x - x 1 ) ( x - x 2 )
Áp dụng : phân tích đa thức thành nhân tử.
a ) 2 x 2 - 5 x + 3 ; b ) 3 x 2 + 8 x + 2
* Chứng minh:
Phương trình a x 2 + b x + c = 0 có hai nghiệm x 1 ; x 2
⇒ Theo định lý Vi-et: 
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
= 
= a . x 2 + b x + c ( đ p c m ) .
* Áp dụng:
a) 2 x 2 – 5 x + 3 = 0
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm 
Vậy: 
b) 3 x 2 + 8 x + 2 = 0
Có a = 3; b' = 4; c = 2
⇒ Δ ’ = 4 2 – 2 . 3 = 10 > 0
⇒ Phương trình có hai nghiệm phân biệt:

Đúng 0
Bình luận (0)
cho phương trình ax2 + bx + c = 0 vô nghiệm ( a>0)
CMR: ax2 + bx + c > 0 với mọi x thuộc R
Vì PTVN nên Δ<0
=>f(x)=ax^2+bx+c luôn cùng dấu với a
=>f(x)>0 với mọi x
Đúng 0
Bình luận (0)
tìm điều kiện của a,b,c để phương trình sau vô nghiệm:
a(ax2+bx+c)2+b(ax2+bx+c)+c=x
Có bao nhiêu cặp số nguyên (a;b) với
a
,
b
∈
0
;
10
để phương trình
x
2
+
a
x
+
b
2
+
a
x
2...
Đọc tiếp
Có bao nhiêu cặp số nguyên (a;b) với a , b ∈ 0 ; 10 để phương trình x 2 + a x + b 2 + a x 2 + a x + b + b = x có bốn nghiệm thực phân biệt.
A.33
B. 32
C. 34
D. 31
Trong các cặp số thực (a;b) để bất phương trình:
x
-
1
x
-
a
x
2
+
x
+
b
≥
0
nghiệm đúng
∀
x
∈
R
tích ab nhỏ nhất bằng A. 1 B. -2 C.
-...
Đọc tiếp
Trong các cặp số thực (a;b) để bất phương trình: x - 1 x - a x 2 + x + b ≥ 0 nghiệm đúng ∀ x ∈ R tích ab nhỏ nhất bằng
A. 1
B. -2
C. - 1 4
D. 1 4
Chứng tỏ rằng nếu phương trình ax2 + bx + c = 0 có nghiệm là x1 và x2 thì tam thức ax2 + bx + c phân tích được thành nhân tử như sau:
ax2 + bx + c = a( x - x1)(x - x2)
Áp dụng : phân tích đa thức thành nhân tử.
3x2 + 8x + 2
3x2 + 8x + 2 = 0
Có a = 3; b' = 4; c = 2
⇒ Δ’ = 42 – 2.3 = 10 > 0
⇒ Phương trình có hai nghiệm phân biệt:

Đúng 0
Bình luận (0)
3. Viết hệ thức Vi-et đối với các nghiệm của phương trình bậc hai
a
x
2
+
b
x
+
c
0
(
a
≠
0
)
Nêu điều kiện để phương trình
a
x
2
+
b
x
+
c
0
(a ≠...
Đọc tiếp
3. Viết hệ thức Vi-et đối với các nghiệm của phương trình bậc hai
a x 2 + b x + c = 0 ( a ≠ 0 )
Nêu điều kiện để phương trình a x 2 + b x + c = 0 (a ≠ 0) có một nghiệm bằng 1. Khi đó, viết công thức nghiệm thứ hai. Áp dụng: nhẩm nghiệm của phương trình
1954 x 2 + 21 x – 1975 = 0
Nêu điều kiện để phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có một nghiệm bằng -1. Khi đó, viết công thức nghiệm thứ hai. Áp dụng: nhẩm nghiệm của phương trình
2005 x 2 + 104 x – 1901 = 0