
Những câu hỏi liên quan
Cho ∆ABC có a=2 b=1 và góc C=60°.Tính c ,góc A,góc B,p,S,ha,R,r,ma,mb,mc
Cho tam giác ABC có b = 7 ,c = 5 và cos A = \(\dfrac{3}{5}\). Tính a , sin A, diện tích S của ABC, R, r, ha
\(a^2=b^2+c^2-2bc.\cos A\Rightarrow a=\sqrt{b^2+c^2-2bc.cosA}=\sqrt{7^2+5^2-\dfrac{2.7.5.3}{5}}=4\sqrt{2}\)
\(\sin A=\sqrt{1-cos^2A}=\sqrt{1-\left(\dfrac{3}{5}\right)^2}=\dfrac{4}{5}\)
\(p=\dfrac{a+b+c}{2}=6+2\sqrt{2}\)
\(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}=14\)
\(R=\dfrac{a}{2.sinA}=\dfrac{4\sqrt{2}}{\dfrac{2.4}{5}}=\dfrac{5\sqrt{2}}{2}\)
\(r=\dfrac{S}{p}=\dfrac{14}{6+2\sqrt{2}}=3-\sqrt{2}\)
\(ha=\dfrac{2S}{a}=\dfrac{2.14}{4\sqrt{2}}=2\sqrt{2}\)
Đúng 1
Bình luận (0)
\(\cos A=\dfrac{b^2+c^2-a^2}{2bc}\)
\(\Leftrightarrow7^2+5^2-a^2=\dfrac{3}{5}\cdot2\cdot7\cdot5=3\cdot2\cdot7=42\)
\(\Leftrightarrow a^2=32\)
hay \(a=4\sqrt{2}\)
\(\sin A=\sqrt{1-\left(\dfrac{3}{5}\right)^2}=\dfrac{4}{5}\)
Đúng 2
Bình luận (0)
Bài 10:Cho ABC có a 8, b 10, c 13 a. ABC có góc tù hay không ? Tính bán kính đường tròn ngoại tiếp ABC. b. Tính diện tích ABC Bài 11:Cho tam giác ABC có: a 6, b 7, c 5. a) Tính S ,h ,R,r ABC a b) Tính bán kính đường tròn đi qua A, C và trung điểm M của cạnh AB.Bài 12:Cho tam giác ABC có: AB 6, BC 7, AC 8. M trên cạnh AB sao cho MA 2 MB. a) Tính các góc của tam giác ABC. b) Tính S ,h ,R ABC a , r. c) Tính bán kính đường tròn ngoại tiếp ∆MBC.Bài 13:Cho ABC có 0 0 A B b 60 , 45 , 2...
Đọc tiếp
Bài 10:Cho ABC có a = 8, b =10, c =13 a. ABC có góc tù hay không ? Tính bán kính đường tròn ngoại tiếp ABC. b. Tính diện tích ABC
Bài 11:Cho tam giác ABC có: a = 6, b = 7, c = 5. a) Tính S ,h ,R,r ABC a b) Tính bán kính đường tròn đi qua A, C và trung điểm M của cạnh AB.
Bài 12:Cho tam giác ABC có: AB = 6, BC = 7, AC = 8. M trên cạnh AB sao cho MA = 2 MB. a) Tính các góc của tam giác ABC. b) Tính S ,h ,R ABC a , r. c) Tính bán kính đường tròn ngoại tiếp ∆MBC.
Bài 13:Cho ABC có 0 0 A B b = = = 60 , 45 , 2 tính độ dài cạnh a, c, bán kính đường tròn ngoại tiếp và diện tích tam giác ABC
Bài 14:Cho ABC AC = 7, AB = 5 và 3 cos 5 A = . Tính BC, S, a h , R, r.
Bài 15:Cho ABC có 4, 2 m m b c = = và a =3 tính độ dài cạnh AB, AC.
Bài 16:Cho ABC có AB = 3, AC = 4 và diện tích S = 3 3 . Tính cạnh BC
Bài 17:Cho tam giác ABC có ˆ o A 60 = , c h 2 3 = , R = 6. a) Tính độ dài các cạnh của ∆ABC. b) Họi H là trực tâm tam giác ABC. Tính bán kính đường tròn ngoại tiếp ∆AHC.
Bài 18:a. Cho ABC biết 0 0 a B C = = = 40,6; 36 20', 73 . Tính BAC , cạnh b,c. b.Cho ABC biết a m = 42,4 ; b m = 36,6 ; 0 C = 33 10' . Tính AB, và cạnh c.
Bài 19:Tính bán kính đường tròn nội tiếp ABC biết AB = 2, AC = 3, BC = 4.
Bài 20:Cho ABC biết A B C (4 3; 1 , 0;3 , 8 3;3 − ) ( ) ( ) a. Tính các cạnh và các góc của ABC b. Tính chu vi và diện tích ABC
Cho tam giác ABC có \(\widehat{A}\) = 120°, b = 8 cm, c = 5 cm. Tính a, \(\widehat{B}\), \(\widehat{C}\), ha, mc, S, R, r
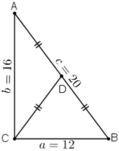
Cho tam giác ABC có a = 12, b = 16, c = 20. Tính diện tích S của tam giác, chiều cao ha, bán kính R, r của các đường tròn ngoại tiếp, nội tiếp tam giác và đường trung tuyến ma của tam giác
Nhận xét: Tam giác ABC có a2 + b2 = c2 nên vuông tại C.
+ Diện tích tam giác: S = 1/2.a.b = 1/2.12.16 = 96 (đvdt)
+ Chiều cao ha: ha = AC = b = 16.
+ Tâm đường tròn ngoại tiếp tam giác là trung điểm của AB.
Bán kính đường tròn ngoại tiếp R = AB /2 = c/2 = 10.
+ Bán kính đường tròn nội tiếp tam giác: S = p.r ⇒ r = S/p.
Mà S = 96, p = (a + b + c) / 2 = 24 ⇒ r = 4.
+ Đường trung tuyến ma:
ma2 = (2.(b2 + c2) – a2) / 4 = 292 ⇒ ma = √292.
Đúng 0
Bình luận (0)
cho tam giác ABC có c=5 ; a= 7 ; góc B=120° Tính: S , AC, ha , R
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot BA\cdot BC\cdot sinABC\)
\(=\dfrac{1}{2}\cdot5\cdot7\cdot sin120=\dfrac{35\sqrt{3}}{4}\)
Xét ΔABC có \(cosB=\dfrac{BA^2+BC^2-AC^2}{2\cdot BA\cdot BC}\)
=>\(\dfrac{5^2+7^2-AC^2}{2\cdot5\cdot7}=cos120=\dfrac{-1}{2}\)
=>\(25+49-AC^2=-35\)
=>\(AC^2=25+49+35=109\)
=>\(AC=\sqrt{109}\)
Kẻ AH\(\perp\)BC
=>\(h_A=AH\)
\(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC\)
=>\(\dfrac{1}{2}\cdot AH\cdot7=\dfrac{35\sqrt{3}}{4}\)
=>\(AH\cdot3,5=\dfrac{35\sqrt{3}}{4}\)
=>\(AH=\dfrac{10\sqrt{3}}{4}=\dfrac{5}{2}\sqrt{3}\)
Xét ΔABC có \(\dfrac{AC}{sinB}=2R\)
=>\(2R=\dfrac{\sqrt{109}}{sin120}=\sqrt{109}\cdot\dfrac{2}{\sqrt{3}}\)
=>\(R=\sqrt{\dfrac{109}{3}}=\dfrac{\sqrt{327}}{3}\)
Đúng 2
Bình luận (0)
1. Cho tam giác ABC có a \(=4\sqrt{2}\), c \(=10\), B\(=45^0\). Tính b, cos C, S, R, sin A, ha
Theo định lí hàm sin, ta có:
A
B
sin
ˆ
C
=
A
C
sin
ˆ
B
⇔
5
sin
45
°
=
A
C
sin
60
°
⇒
A
C
=
5.
sin
60
0
sin
45
0
=
5
√
6
2
.
Đúng 0
Bình luận (0)
cho tam giac ABC...cạnh b=8cm, c=5, gocA=60°..tinh S, R, r, ha, ma
(1) ta có : \(S_{\Delta ABC}=\dfrac{1}{2}.b.c.sinA=\dfrac{1}{2}.8.5.sin60^0=10\sqrt{3}\)
(2) ta có : \(a^2=b^2+c^2-2bc.cosA=8^2+5^2-2.8.5.cos60\)
\(\Leftrightarrow a^2=49\Leftrightarrow a=\sqrt{49}=7\)
ta có : \(S_{\Delta ABC}=\dfrac{abc}{4R}\Leftrightarrow10\sqrt{3}=\dfrac{7.8.5}{4R}\Leftrightarrow R=\dfrac{7.8.5}{4.10\sqrt{3}}=\dfrac{7\sqrt{3}}{3}\)
(3) ta có : \(p=\dfrac{7+8+5}{2}=10\)
ta có : \(S_{\Delta ABC}=p.r\Leftrightarrow10\sqrt{3}=10.r\Leftrightarrow r=\dfrac{10\sqrt{3}}{10}=\sqrt{3}\)
(4) ta có : \(S_{\Delta ABC}=\dfrac{1}{2}a.h_a\Leftrightarrow10\sqrt{3}=\dfrac{1}{2}.7.h_a\Leftrightarrow h_a=10\sqrt{3}.\dfrac{2}{7}=\dfrac{20\sqrt{3}}{7}\)
(5) ta có : \(\left(m_a\right)^2=\dfrac{b^2+c^2}{2}-\dfrac{a^2}{4}=\dfrac{8^2+5^2}{2}-\dfrac{7^2}{4}=\dfrac{129}{4}\)
\(\Leftrightarrow m_a=\sqrt{\dfrac{129}{4}}=\dfrac{\sqrt{129}}{2}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có a=7; b=5; góc C=50°. Tìm c, S, R, ha






















