
Những câu hỏi liên quan
Cho góc XOy khác góc bẹt.
CMR: góc xOy < 180°
ta có góc bẹt bằng 180 độ và là góc lớn nhất
mà xOy khác góc bẹt
nên góc xOy < 180 độ
Đúng 0
Bình luận (0)
Cho hình vẽ. Biết góc xOy đối đỉnh với góc xOy, biết
x
O
y
^
O
1
^
165
o
. Tính các góc đỉnh O (khác góc bẹt) A.
O
2
^
165
°
;
O
3...
Đọc tiếp
Cho hình vẽ. Biết góc xOy' đối đỉnh với góc x'Oy, biết x O y ' ^ = O 1 ^ = 165 o . Tính các góc đỉnh O (khác góc bẹt)
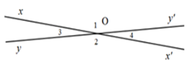
A. O 2 ^ = 165 ° ; O 3 ^ = 15 ° ; O 4 ^ = 165 °
B. O 2 ^ = 165 ° ; O 3 ^ = 15 ° ; O 4 ^ = 15 °
C. O 2 ^ = 15 ° ; O 3 ^ = 15 ° ; O 4 ^ = 165 °
D. O 2 ^ = 15 ° ; O 3 ^ = 165 ° ; O 4 ^ = 15 °
Cho hình vẽ. Biết góc xOy đối đỉnh với góc xOy, biết
x
O
y
^
O
4
^
20
o
. Tính các góc đỉnh O (khác góc bẹt) A.
O
1
^
20
°
;
O
2
^...
Đọc tiếp
Cho hình vẽ. Biết góc xOy' đối đỉnh với góc x'Oy, biết x O y ^ = O 4 ^ = 20 o . Tính các góc đỉnh O (khác góc bẹt)
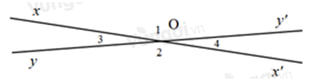
A. O 1 ^ = 20 ° ; O 2 ^ = 160 °
B. O 1 ^ = O 2 ^ = 160 °
C. O 1 ^ = 160 ° ; O 2 ^ = 100 °
D. O 1 ^ = O 2 ^ = 20 °
Cho góc xOy khác góc bẹt. Dùng một chiếc thước thẳng có chia khoảng, hãy nêu cách vẽ tia phân giác của góc xOy.
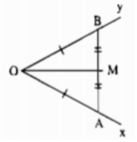
- Dùng thước chia khoảng, trên Ox lấy điểm A, trên Oy lấy điểm B sao cho OA = OB.
- Nối AB.
- Dùng thước chia khoảng để đo đoạn AB, lấy trung điểm M của AB.
- Kẻ tia OM.
Khi đó, OM là tia phân giác của góc ∠xOy.
Chứng minh
Tam giác ABO có OA = OB ( cách dựng) nên tam giác OAB cân tại O.
Lại có: OM là đường trung tuyến nên OM cũng là đường phân giác của ∠(AOB). ( tính chất tam giác cân)
Vậy OM là tia phân giác của ∠(xOy).
Đúng 0
Bình luận (0)
Cho góc xOy khác góc bẹt, trong góc xOy vẽ 2017 tia phân biệt chung gốc O ( khác tia Ox, Oy), hỏi có bao nhiêu góc đỉnh O ở hình vẽ đó?
Vì góc xOy là góc bẹt nên sẽ có 2 cạnh Ox và Oy cộng với 2017 tia còn lại thành 2019 tia
Chọn 1 tia trong 2019 tia nối với 2018 tia còn lại ta đc 2019 nhân 2018 góc mà mỗi góc đc tính 2 lần nên số góc vẽ đc là
2019 nhân 2018 chia 2 =2037171 góc
Đáp số 2037171
sai thì thôi nhé
Đúng 0
Bình luận (0)
Cho góc xOy khác góc bẹt. Dùng một chiếc thước thẳng có chia khoảng, hãy nêu cách vẽ tia phân giác của góc xOy ?
1.Vẽ đường thẳng a song song với Ox
2.Vẽ đường thẳng b song song với Oy
3.Gọi giao điểm của a và b là M
4. Nối O với M. Đó chính là đường phân giác của góc xOy
Đúng 0
Bình luận (0)
Cho góc xOy ( khác góc bẹt) . Gọi I là một điểm nằm tong góc xOy ( I khác O ). Kẻ IH vuông góc với Ox, kẻ Ik vuông góc với Oy , sao cho IH = IK
a) C/m: tam giác OIH = tam giác OIK
b) C/m: OI là tia phân giác của góc xOy
`a)`
Có `IH⊥Ox=>hat(H_1)=90^0`
`IK⊥Oy=>hat(K_1)=90^0`
Xét `Delta KIO` và `Delta HIO` có :
`{:(hat(K_1)=hat(H_1)(=90^0)),(OI-chung),(IK=IH(GT)):}}`
`=>Delta KIO=Delta HIO(c.h-c.g.v)(đpcm)`
`b)`
Có `Delta KIO=Delta HIO(cmt)=>hat(O_1)=hat(O_2)` ( 2 góc t/ứng )
mà `OI` nằm giữa `Ox` và `Oy(I in hat(xOy))`
nên `OI` là p/g của `hat(xOy)(đpcm)`
Đúng 1
Bình luận (0)
Cho góc xOy khác góc bẹt. Lấy các điểm A,B thuộc tia Ox sao cho OA
Xem chi tiết
Cho xOy khác góc bẹt. Vẽ Ox vuông góc với O'x', Oy vuông góc với O'y'. CMR góc xOy + góc x'O'y' = 180 độ và
xOy= x'O'y
















