rút gọn biểu thức B=gá trị tuyệt đối của x+10/x64+9x^3-9x^2+9x-10
Những câu hỏi liên quan
Cho biểu thức: B=\(\dfrac{\left|x+10\right|}{x^4+9x^3-9x^2+9x-10}\)
a) Tìm điều kiện có nghĩa của B
b) Rút gọn B
21 tháng 12 2023 lúc 18:00
Bài 1: Tìm x; biết:
a) 2x^2-8x=0 b) (x+2)^2-x(x-1)=10 c)b x^3-6x^2+9x=0
Bài 2: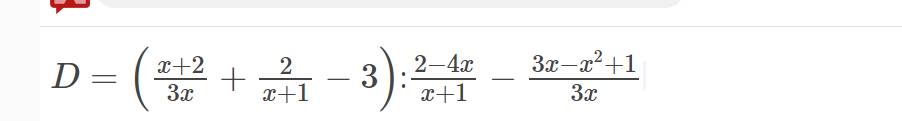
a) Viết điều kiện xác định của biểu thức D
b) Rút gọn biểu thức D
c) Tính giá trị của D khi x=1/
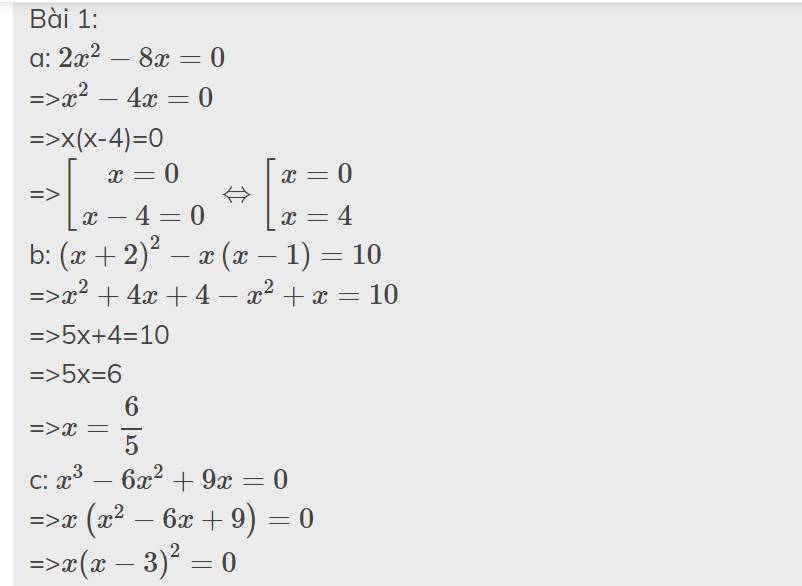
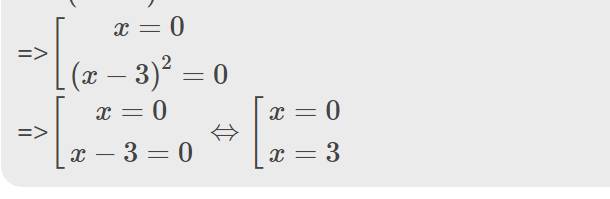Bài 2:
a: ĐKXĐ: \(x\notin\left\{0;-1;\dfrac{1}{2}\right\}\)
b: \(D=\left(\dfrac{x+2}{3x}+\dfrac{2}{x+1}-3\right):\dfrac{2-4x}{x+1}-\dfrac{3x-x^2+1}{3x}\)
\(=\dfrac{\left(x+2\right)\left(x+1\right)+6x-3\cdot3x\left(x+1\right)}{3x\left(x+1\right)}\cdot\dfrac{x+1}{2-4x}+\dfrac{x^2-3x-1}{3x}\)
\(=\dfrac{x^2+3x+2+6x-9x^2-9x}{3x}\cdot\dfrac{1}{2-4x}+\dfrac{x^2-3x-1}{3x}\)
\(=\dfrac{-8x^2+2}{3x}\cdot\dfrac{1}{-4x+2}+\dfrac{x^2-3x-1}{3x}\)
\(=\dfrac{-2\left(2x-1\right)\left(2x+1\right)}{3x\cdot\left(-2\right)\left(2x-1\right)}+\dfrac{x^2-3x-1}{3x}\)
\(=\dfrac{2x+1}{3x}+\dfrac{x^2-3x-1}{3x}\)
\(=\dfrac{2x+1+x^2-3x-1}{3x}=\dfrac{x^2-x}{3x}=\dfrac{x-1}{3}\)
c: Khi x=1 thì \(D=\dfrac{1-1}{3}=0\)
Đúng 0
Bình luận (0)
Bài 4 : Rút gọn rồi tính giá trị của biểu thức:
a/ (x - 10)2 - x(x+80) khi x=0,98
b/ x3 - 9x + 27x - 27 khi x=5
a)(x-10)2-x(x+80)
(x2-2x10+100)-x2-80x
=x2-20x+100-x2-80x=-100x+100
khi x = 0.98
ta có
(-100*0.98)+100=-98+100=2
b)x3-9x+27x-27
hình như là -27x :))
Đúng 0
Bình luận (0)
21 tháng 12 2023 lúc 19:06
Bài 1: Tìm x; biết:
a) 2x^2-8x=0 b) (x+2)^2-x(x-1)=10 c)b x^3-6x^2+9x=0
Bài 2:
a) Viết điều kiện xác định của biểu thức D
b) Rút gọn biểu thức D
c) Tính giá trị của D khi x=1/2
Bài 1:
a: \(2x^2-8x=0\)
=>\(x^2-4x=0\)
=>x(x-4)=0
=>\(\left[{}\begin{matrix}x=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
b: \(\left(x+2\right)^2-x\left(x-1\right)=10\)
=>\(x^2+4x+4-x^2+x=10\)
=>5x+4=10
=>5x=6
=>\(x=\dfrac{6}{5}\)
c: \(x^3-6x^2+9x=0\)
=>\(x\left(x^2-6x+9\right)=0\)
=>\(x\left(x-3\right)^2=0\)
=>\(\left[{}\begin{matrix}x=0\\\left(x-3\right)^2=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)
Đúng 2
Bình luận (0)
A=\(\frac{|x+10|}{x^4+9x^3-9x^2+9x-10}\)
tìm điều kiện và rút gọn B
Câu1: Rút gọn biểu thức:
a) 2x^2(x^2+3x+1/2)
b) (x+1)(x-2)-(x+2)^2
c) (3x+1)^2 -9x(x+3)
Câu2: Chứng minh giá trị của các biểu thức sau không phụ thuộc vào giá trị của biến.
a) (x+2)^2 -x(x+4)+10
b) (x+3)(4x-1)-(2x+1)^2 -7x+3
Câu3: Tìm x, biết:
a) (x+2)^2 -x(x-1)2
b) (2x+1)^2 -(x+1)(4x-3) -3
Câu5: Cho hình thang cân ABCD hai đáy là AB và CD, gọi O là giao điểm hai đường chéo. C/m rằng: OAOB; OCOD.
Đọc tiếp
Câu1: Rút gọn biểu thức:
a) 2x^2(x^2+3x+1/2)
b) (x+1)(x-2)-(x+2)^2
c) (3x+1)^2 -9x(x+3)
Câu2: Chứng minh giá trị của các biểu thức sau không phụ thuộc vào giá trị của biến.
a) (x+2)^2 -x(x+4)+10
b) (x+3)(4x-1)-(2x+1)^2 -7x+3
Câu3: Tìm x, biết:
a) (x+2)^2 -x(x-1)=2
b) (2x+1)^2 -(x+1)(4x-3)= -3
Câu5: Cho hình thang cân ABCD hai đáy là AB và CD, gọi O là giao điểm hai đường chéo. C/m rằng: OA=OB; OC=OD.
Câu 1:
a: \(2x^2\left(x^2+3x+\frac12\right)\)
\(=2x^2\cdot x^2+2x^2\cdot3x+2x^2\cdot\frac12\)
\(=2x^4+6x^3+x^2\)
b: \(\left(x+1\right)\left(x-2\right)-\left(x+2\right)^2\)
\(=x^2-2x+x-2-\left(x^2+4x+4\right)\)
\(=x^2-x-2-x^2-4x-4=-5x-6\)
c: \(\left(3x+1\right)^2-9x\left(x+3\right)\)
\(=9x^2+6x+1-9x^2-27x\)
=-21x+1
Câu 2:
a: \(\left(x+2\right)^2-x\left(x+4\right)+10\)
\(=x^2+4x+4-x^2-4x+10\)
=4+10
=14
=>Biểu thức này không phụ thuộc vào biến
b: \(\left(x+3\right)\left(4x-1\right)-\left(2x+1\right)^2-7x+3\)
\(=4x^2-x+12x-3-4x^2-4x-1-7x+3\)
=12x-x-7x-4x-3-1+3
=x(12-1-7-4)-1
=-1
=>Biểu thức này không phụ thuộc vào biến
Câu 3:
a: \(\left(x+2\right)^2-x\left(x-1\right)=2\)
=>\(x^2+4x+4-x^2+x=2\)
=>5x+4=2
=>5x=2-4=-2
=>\(x=-\frac25\)
b: \(\left(2x+1\right)^2-\left(x+1\right)\left(4x-3\right)=-3\)
=>\(4x^2+4x+1-\left(4x^2-3x+4x-3\right)=-3\)
=>\(4x^2+4x+1-\left(4x^2+x-3\right)=-3\)
=>\(4x^2+4x+1-4x^2-x+3=-3\)
=>3x+4=-3
=>3x=-7
=>\(x=-\frac73\)
Câu 5
Xét ΔADC và ΔBCD có
AD=BC
DC chung
AC=BD
Do đó: ΔADC=ΔBCD
=>\(\hat{ACD}=\hat{BDC}\)
=>\(\hat{OCD}=\hat{ODC}\)
=>ΔOCD cân tại O
=>OC=OD
Ta có: OC+OA=AC
OD+OB=BD
mà OC=OD và AC=BD
nên OA=OB
Đúng 0
Bình luận (0)
F=x^13-9x^12+9x^11-9x^10+.....-9x^2+9x-2 với x=8
Tính giá trị biểu thức trên 1 cách hợp lý
x=8 nên x+1=9
\(F=x^{13}-9x^{12}+9x^{11}-9x^{10}+...-9x^2+9x-2\)
\(=x^{13}-x^{12}\left(x+1\right)+x^{11}\left(x+1\right)-x^{10}\left(x+1\right)+...-x^2\left(x+1\right)+x\left(x+1\right)-2\)
\(=x^{13}-x^{13}-x^{12}+x^{12}+...-x^3-x^2+x^2+x-2\)
=x-2
=8-2
=6
Đúng 0
Bình luận (0)
Cho biểu thức :
\(P=\dfrac{1}{x+5}+\dfrac{2}{x-5}-\dfrac{2x+10}{x^2-25}\)
a) Rút gọn P
b) Cho P=-3. Tính giá trị của biểu thức Q=9x2-42x+49
c) Tìm số tự nhiên x để P nguyên
các bạn đi học chưa hả?
Xem thêm câu trả lời
Rút gọn phân thức x^2-2x-8/2x^2+9x+10
\(\dfrac{x^2-2x-8}{2x^2+9x+10}\)
\(=\dfrac{x^2-4x+2x-8}{2x^2+4x+5x+10}\)
\(=\dfrac{\left(x-4\right)\left(x+2\right)}{\left(x+2\right)\left(2x+5\right)}\)
\(=\dfrac{x-4}{2x+5}\)
Đúng 0
Bình luận (0)