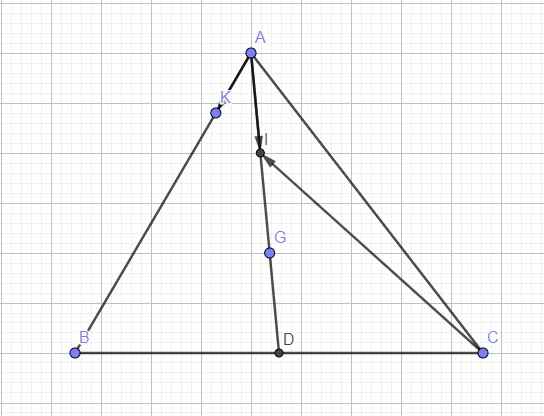
1, Cho tam giác ABC có G là trọng tâm, biết rằng vecto AG= x vecto AB + y vecto AC (x;y ∈ R). tính T=x+y.
2, cho tam giác ABC đều cạnh a, H là trung điểm của BC. Tính |vecto CA - vecto HC|.
3, Cho tập hợp A= x ∈ R; x=3k, k ∈ Z, 10<x<100. Tổng các phần tử của tập hợp A bằng bao nhiêu?