
Những câu hỏi liên quan
Cho ΔABC cân tại A, có AB < BC. Trên BC lấy M,N sao cho BM=CN=AB:
CMR: a, ΔAMN cân
b, Tính số đo các góc của ΔAMN khi góc BAC = 120°
c, Có khi nào Δ AMN là Tam giác vuông cân Đc hay ko?
cho ΔEMN cân tại E (góc E<90 độ).các đướng cao MA,NB cắt nhau tại I .tia EI cắt MN tại H
a)chứng minh :ΔAMN=ΔBMN
b)chứng minh EH là trung tuyến của ΔEMN
c)Tính dộ dài đoạn thẳng MA biết AN = 3cm,AE = 2cm
d)chứng minh i cách đều 3 cạnh của ΔABH
a) Xét ΔANM vuông tại A và ΔBMN vuông tại B có
MN chung
\(\widehat{ANM}=\widehat{BMN}\)(ΔEMN cân tại E)
Do đó: ΔANM=ΔBMN(Cạnh huyền-góc nhọn)
b) Xét ΔEMN có
MA là đường cao ứng với cạnh EN(gt)
NB là đường cao ứng với cạnh EM(gt)
MA cắt NB tại I(Gt)
Do đó: I là trực tâm của ΔEMN(Tính chất ba đường cao của tam giác)
Suy ra: EI\(\perp\)MN tại H
Xét ΔEMH vuông tại H và ΔENH vuông tại H có
EM=EN(ΔEMN cân tại E)
EH chung
Do đó: ΔEMH=ΔENH(Cạnh huyền-cạnh góc vuông)
Suy ra: MH=NH(Hai cạnh tương ứng)
mà M,H,N thẳng hàng(gt)
nên H là trung điểm của MN
hay EH là đường trung tuyến của ΔMNE(đpcm)
Đúng 3
Bình luận (0)
Cho tam giác ABC có ba góc nhọn, biết
A
B
15
c
m
,
A
C
13
c
m
và đường cao
A
H
12
c
m
.
Gọi N, M lần lượt là hình chiếu vuông góc của H xuống AC và AB.a) Chứng minh rằng ΔAHN ∼ ΔACHb) Tính độ dài BCc) Chứng minh ΔAMN ∼ ΔACBd) Tính MN
Đọc tiếp
Cho tam giác ABC có ba góc nhọn, biết A B = 15 c m , A C = 13 c m và đường cao A H = 12 c m . Gọi N, M lần lượt là hình chiếu vuông góc của H xuống AC và AB.
a) Chứng minh rằng ΔAHN ∼ ΔACH
b) Tính độ dài BC
c) Chứng minh ΔAMN ∼ ΔACB
d) Tính MN
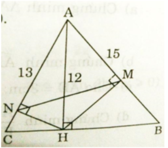
a) Xét ΔANH và ΔAHC có:
∠(NAH) chung
∠(ANH) = ∠(AHN) = 90o
⇒ ΔANH ∼ ΔAHC (g.g)
b) Ta có :
![]()
![]()
Tương tự : CH = 5 (cm)
⇒ BC = BH + CH = 9 + 5 = 14 (cm)
c) Theo chứng minh trên ta có:
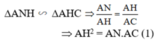
Chứng minh tương tự ta có :
ΔAMH ∼ ΔAHB ⇒ AH2 = AM.AB (2)
Từ (1) và (2) ⇒ AN.AC = AM.AB (3)
Xét ΔAMN và ΔACB có :
∠A chung
AN.AC = AM.AB
⇒ ΔAMN ∼ ΔACB (c.g.c)
d) Ta có : ΔAMH ∼ ΔAHB
![]()
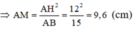
Lại có ΔAMN ∼ ΔACB (cmt)
![]()
![]()
Đúng 0
Bình luận (0)
Cho ΔABC nhọn. Đường cao BE, CF cắt nhau ở H.
a/ Cm: AE.AC = AF.AB
b/ Cm: BH.BE + CH.CF = \(BC^2\)
c/ Trên đoạn BH, CH lần lượt lấy M, N sao cho góc AMC = góc ANB = \(90^o\). Cm: ΔAMN cân
a) Xét tam giác AFC và tam giác AEB có:
^A chung
^F vuông góc ^E
Vậy: tam giác AFC đồng dạng tam giác AEB (g.g)
vì tam giác AFC đồng dạng tam giác AEB (cmt) nên:
=> AF/AC = AE/AB
=> AE.AC = AF.AB (đpcm)
b) từ H kẻ HK vuông góc BC
+) xét tam giác BKH và tam giác BEC có:
^HBC chung
^BKH = ^BEC (= 90 độ)
vậy: tam giác BKH đồng dạng tam giác BEC (g.g)
=> BK/BH = BE/BC
=> BH.BE = BK.BC (1)
+) xét tam giác CKH và tam giác CFB:
^BHC chung
^CKH = ^CFB (= 90 độ)
vậy: tam giác CKH đồng dạng tam giác CFB
=> CK/CH = CF/CB
=> CH.CF = BC.CK (2)
Từ (1) và (2) ta có:
BH.BE + CH.CF = BK.BC + CK.BC
= BC.(BK + CK)
= BC.BC
= BC^2
=> BH.BE + CH.CF = BC^2 (đcpm)
Cho hình thang vuông ABCD có góc A Góc D 90 độ, E,F thuộc AD, AE DF, góc BFC 90 độ. Chứng minh góc BÉC 90 độ
Cho hình thang vuông ABCD có góc A = Góc D = 90 độ, E,F thuộc AD, AE=DF, góc BFC = 90 độ. Chứng minh góc BÉC = 90 độ
ΔABC cân tại A, lấy MϵAB, NϵAC, sao cho AM=AN.
a) Tìm góc M, góc B theo góc A. Chứng minh ΔAMN cân
b) Chứng minh MN//BC
a, ^M = \(\dfrac{180^0-\widehat{A}}{2}\); ^B = \(\dfrac{180^0-\widehat{A}}{2}\)
Xét tam giác AMN có : AM = AN
nên tam giác AMN cân tại A
b, Vì ^M = ^B = (1800 - ^A)/2
mà 2 góc này ở vị trí đồng vị
=> MN // BC
Đúng 0
Bình luận (0)
cho tam giác ABC có góc A = 90 độ , AD = HE , có AH vuông góc với BC , có DF vuông góc với AH . Chứng minh góc BEF = 90 độ
mình quên viết là trên tia đối của tia AD lấy E sao cho AD = HE nhé ( D thuộc AH đấy )
Đúng 0
Bình luận (0)
Bài 28. Cho ΔEMN cân tại E (E < 90 độ) , các đường cao MA, NB cắt nhau tại I. Tia EI cắt MN tại H.
a) Chứng minh ΔAMN = ΔBNM.
b) Chứng minh EH là đường trung tuyến của ΔEMN.
c) Tính độ dài đoạn thẳng MA biết AN = 3cm, AE = 2cm.
d) Chứng minh I cách đều ba cạnh của ΔABH.
















