Tronng mặt phẳng Oxy, cho hình vuông ABCD có A(1;-1) và B(3;0).Tọa độ các đỉnh C và D là:
A.C(4;-2);D(2;2) hoặc C(2;-4);D(4;-2)
B.C(4;2);D(2;-3) hoặc C(-2;2);D(0;1)
C.C(4;-2);D(2;3) hoặc C(2;2);D(0:1)
D.C(2;-3);D(0;1) hoặc C(0;1);D(2;-3)
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có A(1; -1) và B(3; 0). Tìm tọa độ điểm D, biết D có tung độ âm.
A.D(0; -1)
B. D( 2; -3)
C. D( 2; -3); D(0; 1)
D. D( -2; -3)
Gọi C= (x, y). Ta có A B → = 2 ; 1 B C → = x − 3 ; y .
Vì ABCD là hình vuông nên ta có A B → ⊥ B C → A B = B C
⇔ 2 x − 3 + 1. y = 0 x − 3 2 + y 2 = 5 ⇔ y = 2 3 − x 5 x − 3 2 = 5 ⇔ y = 2 3 − x x − 3 2 = 1 ⇔ x = 4 y = − 2 hoặc x = 2 y = 2 .
Với C 1 4 ; − 2 ta tính được đỉnh D 1 2 ; − 3 : thỏa mãn.
Với C 2 2 ; 2 ta tính được đỉnh D 2 0 ; 1 : không thỏa mãn.
Chọn B.
 Trong mặt phẳng Oxy, cho hình vuông ABCD có đình M(-–-3;5), tâm I thuộc đường thẳng d : y =−x+5 và diện tích của hình vuông ABCD bằng 25 . Tim tọa độ các đỉnh của hình vuông ABCD, biết rằng tâm I có hoành độ dương
Trong mặt phẳng Oxy, cho hình vuông ABCD có đình M(-–-3;5), tâm I thuộc đường thẳng d : y =−x+5 và diện tích của hình vuông ABCD bằng 25 . Tim tọa độ các đỉnh của hình vuông ABCD, biết rằng tâm I có hoành độ dương
Trong mặt phẳng tọa độ Oxy, cho 3 điểm có A(-3;-2); B(3;6); C(11;0). Tìm tọa độ điểm D để tứ giác ABCD là hình vuông
Trong mặt phẳng Oxy, cho bốn điểm \(A(2;1),B(1;4),C(4;5),D(5;2)\)
a) Chứng minh ABCD là một hình vuông
b) Tìm tọa độ tâm I của hình vuông ABCD
a) Ta có: \(\overrightarrow {AB} = ( - 1;3),\overrightarrow {BC} = (3;1),\overrightarrow {CD} = (1; - 3),\overrightarrow {DA} = ( - 3; - 1)\)
Suy ra \(AB = BC = CD = DA = \sqrt {10} \)
Mặt khác \(\overrightarrow {AB} .\overrightarrow {BC} = ( - 1).3 + 3.1 = 0 \Rightarrow AB \bot BC\)
Vậy ABCD là hình vuông
b) Ta có ABCD là hình vuông, nên tâm I là trung điểm của đoạn thẳng AC
Vậy tọa độ điểm I là \(I(3;3)\)

Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có đỉnh A(-3;5), tâm I thuộc đường thẳng ∆ : x + y - 5 = 0 và diện tích hình vuông bằng 25. Tìm tọa độ đỉnh C, biết rằng tâm I có hoành độ dương.
![]()
![]()
![]()
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có đỉnh A(-3;5), tâm I thuộc đường thẳng ∆ : x + y - 5 = 0 và diện tích hình vuông bằng 25. Tìm tọa độ đỉnh C, biết rằng tâm I có hoành độ dương
A. C 9 2 ; - 1 2
B. C(1;8)
C. C(4;4)
D. C(2;2)
1, Cho hình chóp SABCD có đáy ABCD là hình vuông . Mặt bên SAB là tam giác đều nằm trong mặt phẳng vuông góc với (ABCD).CÓ mấy mặt phẳng vuông góc với (sab)
2, Cho hình chóp SABCD có đáy ABCD là hình thoi . Mặt phẳng (SAC) vuông góc (ABCD) . mệnh đề nào đúng
A. (SAC) vuông góc (SBD)
b. (SBD) vuông góc (ABCD)
C.(BCD) vuông góc (ACD)
D.(SAB) vuông góc (SAD)
3, Cho tứ diện ABCD có AB=AC=AD và tam giác BCD vuông ở B . Trong các mặt phẳng sau , cặp nào vuông góc với nhau
A.(ABC) và (ABD) B.(ABD) và (BCD)
C. (BCD) và (ACD) D.(ACD) và (ABC)
4. tứ diện abcd có bcd là tam giác vuông ở b . (ABC) vuông góc (BCD) . các cạnh của tứ diện cạnh nào là đường cao
5. Cho hình chóp SABC có đáy abc là tam giác vuông ở b với AB=3a,BC=4a. biết SA vuông góc với đáy , góc giữa (SBC) và (ABC)=60 ĐỘ . TÍNH diện tích tam giác sbc
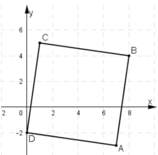
Trên mặt phẳng tọa độ Oxy cho bốn điểm: A(7; -3), B(8; 4), C(1; 5), D(0; –2). Chứng minh rằng tứ giác ABCD là hình vuông.
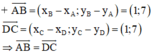
⇒ ABCD là hình bình hành.
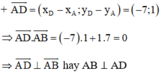
⇒ hình bình hành ABCD là hình chữ nhật.
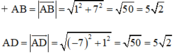
⇒ AB = AD ⇒ Hình chữ nhật ABCD là hình vuông (ĐPCM).
Trong mặt phẳng tọa độ Oxy, cho 3 điểm có A(-3;-2); B(3;6); C(11;0). Tìm tọa độ điểm D để tứ giác ABCD là hình vuông