một thuật toán có thể giải được bao nhiêu bài toán
Những câu hỏi liên quan
Chọn phát biểu đúng :
A. Một bài toán có thể có nhiều thuật toán để giải
B. Một bài toán chỉ có một thuật toán để giải
C. Một thuật toán có thể giải tất cả các bài toán
D. Mọi bài toán không có thuật toán để giải
Xem thêm câu trả lời
Hãy chọn phát biểu Sai? *A.Dãy hữu hạn các thao tác cần thực hiện để giải một bài toán được gọi là thuật toánB.Đối với mỗi bài toán cụ thể chúng ta chỉ có 1 thuật toán duy nhất để giải bài toán đó trên máy tínhC.Việc thực hiện cả 3 bước khi giải bài toán trên máy tính là cần thiết, nhất là đối với bài toán phức tạpD.Xác định bài toán là xác định rõ các điều kiện cho trước và kết quả cần thu được
Đọc tiếp
Hãy chọn phát biểu Sai? *
A.Dãy hữu hạn các thao tác cần thực hiện để giải một bài toán được gọi là thuật toán
B.Đối với mỗi bài toán cụ thể chúng ta chỉ có 1 thuật toán duy nhất để giải bài toán đó trên máy tính
C.Việc thực hiện cả 3 bước khi giải bài toán trên máy tính là cần thiết, nhất là đối với bài toán phức tạp
D.Xác định bài toán là xác định rõ các điều kiện cho trước và kết quả cần thu được
Cho một dãy số nguyên gồm 1000 phần tử đếm trong dãy trên có bao nhiêu số chẵn và thỏa mãn ở vị trí lẻ A. Viết thuật toán để giải bài toán trên B. Dựa vào thuật toán viết chương trình để giải bài toán trên
#include <bits/stdc++.h>
using namespace std;
long long a[1000],n,i,dem;
int main()
{
cin>>n;
dem=0;
for (i=1; i<=n; i++)
{
cin>>x;
if ((i%2==1) and (x%2==0)) dem++;
}
cout<<dem;
return 0;
}
Đúng 0
Bình luận (0)
Câu 3: Vận dụng các kiến thức đã học về thuật toán và các cấu trúc điều khiển giải quyết một số bài toán cụ thể, yêu cầu xác định được:1. Đầu vào và đầu ra của thuật toán?2. Mô tả thuật toán giải quyết yêu cầu trên bằng sơ đồ khối.Ví dụ dạng bài toán cụ thể: + Bài toán tính tổng, tích của 2 số a, b. + Bài toán Tìm ước chung lớn nhất của 2 số a,b. + Bài toán Tìm số lớn nhất trong...
Đọc tiếp
Câu 3: Vận dụng các kiến thức đã học về thuật toán và các cấu trúc điều khiển giải quyết một số bài toán cụ thể, yêu cầu xác định được:
1. Đầu vào và đầu ra của thuật toán?
2. Mô tả thuật toán giải quyết yêu cầu trên bằng sơ đồ khối.
Ví dụ dạng bài toán cụ thể: + Bài toán tính tổng, tích của 2 số a, b.
+ Bài toán Tìm ước chung lớn nhất của 2 số a,b.
+ Bài toán Tìm số lớn nhất trong 2 số a,b.
(Học sinh mô tả thuật toán bằng sơ đồ khối giải các bài toán trên)
Nhanh giúp em vs
1: Bài toán tính tổng tích
Input: a,b
Output: a+b và a-b
Mô tả thuật toán
Bước 1: Nhập a,b
Bước 2: Xuất a+b và a-b
Bước 3: Kết thúc
Đúng 0
Bình luận (0)
11 tháng 5 2022 lúc 20:40
Câu 3: Vận dụng các kiến thức đã học về thuật toán và các cấu trúc điều khiển giải quyết một số bài toán cụ thể, yêu cầu xác định được: 1. Đầu vào và đầu ra của thuật toán? 2. Mô tả thuật toán giải quyết yêu cầu trên bằng sơ đồ khối. Ví dụ dạng bài toán cụ thể: + Bài toán tính tổng, tích của 2 số a, b. + Bài toán Tìm ước chung lớn nhất của 2 số a,b. + Bài toán Tìm số lớn nhất trong 2 số a,b.
Đọc tiếp
Câu 3: Vận dụng các kiến thức đã học về thuật toán và các cấu trúc điều khiển giải quyết một số bài toán cụ thể, yêu cầu xác định được: 1. Đầu vào và đầu ra của thuật toán? 2. Mô tả thuật toán giải quyết yêu cầu trên bằng sơ đồ khối. Ví dụ dạng bài toán cụ thể: + Bài toán tính tổng, tích của 2 số a, b. + Bài toán Tìm ước chung lớn nhất của 2 số a,b. + Bài toán Tìm số lớn nhất trong 2 số a,b.
1: Bài toán tính tổng tích
Input: a,b
Output: a+b và a-b
Mô tả thuật toán
Bước 1: Nhập a,b
Bước 2: Xuất a+b và a-b
Bước 3: Kết thúc
Đúng 0
Bình luận (0)
Cả lớp 4A phải làm một bài kiểm tra toán gồm có 3 bài toán. Giáo viên chủ nhiệm lớp báo cáo với nhà trường rằng : cả lớp mỗi em đều làm được ít nhất một bài, trong lớp có 20 em giải được bài toán thứ nhất, 14 em giải được bài toán thứ hai, 10 em giải được bài toán thứ ba, 5 em giải được bài toán thứ hai và thứ ba, 2 em giải được bài toán thứ nhất và thứ hai, có mỗi một em được 10 điểm vì đã giải được cả ba bài. Hỏi rằng lớp học đó có bao nhiêu em tất cả?
Đọc tiếp
Cả lớp 4A phải làm một bài kiểm tra toán gồm có 3 bài toán. Giáo viên chủ nhiệm lớp báo cáo với nhà trường rằng : cả lớp mỗi em đều làm được ít nhất một bài, trong lớp có 20 em giải được bài toán thứ nhất, 14 em giải được bài toán thứ hai, 10 em giải được bài toán thứ ba, 5 em giải được bài toán thứ hai và thứ ba, 2 em giải được bài toán thứ nhất và thứ hai, có mỗi một em được 10 điểm vì đã giải được cả ba bài. Hỏi rằng lớp học đó có bao nhiêu em tất cả?
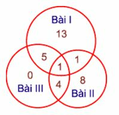
Mỗi hình tròn để ghi số bạn giải đúng một bài nào đó. Vì chỉ có một bạn giải đúng 3 bài nên điền số 1 vào phần chung của 3 hình tròn. Số bạn giải đúng bài I và bài II là 2 nên phần chung của hai hình tròn này mà không chung với hình tròn còn lại sẽ được ghi số 1 (vì 2 - 1 = 1). Tương tự, ta ghi được các số vào các phần còn lại.
Số học sinh lớp 4A chính là tổng các số đã điền vào các phần :
13 + 5 + 1 + 1 + 4 + 8 + 0 = 32 (HS)
Đúng 0
Bình luận (0)
Ba bạn Vui, Học, Toán cùng thi giải toán. Trong cùng một thời gian, Vui giải được 12 bài, Học giải được ít hơn trung bình của 3 bạn là 1 bài; Toán giải được nhiều hơn trung bình của 3 bạn là 5 bài. Hỏi: a. Trung bình mỗi bạn giải được bao nhiêu bài toán? b. Học và Toán đã giải được bao nhiêu bài toán?
ta có : tổng số bài của Học và toán nhiều hơn trung bình ba bạn là 4 bài
Do đó trung bình của ba bạn là \(12+4=16\) bài
Học đã gải được \(16-1=15\) bài
Toán đã giải được \(16+5=21\)bà
cùng nhau cố gắng thôi các bạn ở lớp 4B
Xem thêm câu trả lời
Cả lớp 4A phải làm một bài kiểm tra toán gồm có 3 bài toán. Giáo viên chủ nhiệm lớp báo cáo với nhà trường rằng : cả lớp mỗi em đều làm được ít nhất một bài, trong lớp có 20 em giải được bài toán thứ nhất, 14 em giải được bài toán thứ hai, 10 em giải được bài toán thứ ba, 5 em giải toán thứ hai và thứ ba,2 em giải được bài toán thứ nhất và thứ hai, có mỗi một em được 10 điểm vì đã giải được cả ba bài. Hỏi rằng lớp học đó có bao nhiêu em tất cả ?
Đọc tiếp
Cả lớp 4A phải làm một bài kiểm tra toán gồm có 3 bài toán. Giáo viên chủ nhiệm lớp báo cáo với nhà trường rằng : cả lớp mỗi em đều làm được ít nhất một bài, trong lớp có 20 em giải được bài toán thứ nhất, 14 em giải được bài toán thứ hai, 10 em giải được bài toán thứ ba, 5 em giải toán thứ hai và thứ ba,2 em giải được bài toán thứ nhất và thứ hai, có mỗi một em được 10 điểm vì đã giải được cả ba bài. Hỏi rằng lớp học đó có bao nhiêu em tất cả ?
Bài giải
Mỗi hình tròn để ghi số bạn giải đúng một bài nào đó. Vì chỉ có một bạn giải đúng 3 bài nên điền số 1 vào phần chung của 3 hình tròn. Số bạn giải đúng bài I và bài II là 2 nên phần chung của hai hình tròn này mà không chung với hình tròn còn lại sẽ được ghi số 1 (vì 2 - 1 = 1). Tương tự, ta ghi được các số vào các phần còn lại.
Số học sinh lớp 4A chính là tổng các số đã điền vào các phần
13 + 5 + 1 + 1 + 4 + 8 + 0 = 32 (HS)
Đúng 0
Bình luận (0)
Câu 3: Vận dụng các kiến thức đã học về thuật toán và các cấu trúc điều khiển giải quyết một số bài toán cụ thể, yêu cầu xác định được:
1. Đầu vào và đầu ra của thuật toán?
2. Mô tả thuật toán giải quyết yêu cầu trên bằng sơ đồ khối.
Ví dụ dạng bài toán cụ thể: + Bài toán tính tổng, tích của 2 số a, b.
+ Bài toán Tìm ước chung lớn nhất của 2 số a,b.
+ Bài toán Tìm số lớn n...
Đọc tiếp
Câu 3: Vận dụng các kiến thức đã học về thuật toán và các cấu trúc điều khiển giải quyết một số bài toán cụ thể, yêu cầu xác định được:
1. Đầu vào và đầu ra của thuật toán?
2. Mô tả thuật toán giải quyết yêu cầu trên bằng sơ đồ khối.
Ví dụ dạng bài toán cụ thể: + Bài toán tính tổng, tích của 2 số a, b.
+ Bài toán Tìm ước chung lớn nhất của 2 số a,b.
+ Bài toán Tìm số lớn nhất trong 2 số a,b.
(Học sinh mô tả thuật toán bằng sơ đồ khối giải các bài toán trên)