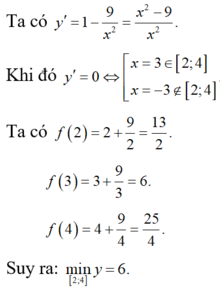Tìm giá trị nhỏ nhất của hàm số \(y=9x\) +\(\dfrac{3x+1}{x-1}\)

Những câu hỏi liên quan
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
\(y=sin\dfrac{2x}{x^2+1}+cos\dfrac{x}{x^2+1}+1\)
tìm giá trị lớn nhất giá trị nhỏ nhất của hàm số trên đoạn [2;4]
y=\(\dfrac{x^2+3}{x-1}\)
Tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
\(y=x^3-3x^2-9x+35\) trên các đoạn [-4; 4] và [0;5] ;
\(y'=3x^2-6x-9=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
a. Trên [-4;4] ta có:
\(y\left(-4\right)=-41\) ; \(y\left(-1\right)=40\) ; \(y\left(3\right)=8\) ; \(y\left(4\right)=15\)
\(\Rightarrow y_{min}=-41\) ; \(y_{max}=40\)
b. Trên [0;5] ta có:
\(y\left(0\right)=35\) ; \(y\left(3\right)=8\); \(y\left(5\right)=40\)
\(\Rightarrow y_{max}=40\) ; \(y_{min}=8\)
Đúng 2
Bình luận (0)
Tìm tất cả các giá trị m để giá trị nhỏ nhất của hàm số:1/ ydfrac{x+m}{x-1} trên left[2;4right] bằng 3.2/ y2x^3-3x^2-m trên left[-1;1right] bằng 1.3/ yleft|x^3-3x^2+mright| trên left[0;3right] bằng 2.
Đọc tiếp
Tìm tất cả các giá trị \(m\) để giá trị nhỏ nhất của hàm số:
1/ \(y=\dfrac{x+m}{x-1}\) trên \(\left[2;4\right]\) bằng 3.
2/ \(y=2x^3-3x^2-m\) trên \(\left[-1;1\right]\) bằng 1.
3/ \(y=\left|x^3-3x^2+m\right|\) trên \(\left[0;3\right]\) bằng 2.
Tìm giá trị nhỏ nhất của hàm số
y
x
+
9
x
trên đoạn
1
;
4
A. B.
min y
1
;
4
−
4
C.
min y
1
;
4...
Đọc tiếp
Tìm giá trị nhỏ nhất của hàm số y = x + 9 x trên đoạn 1 ; 4
A.
B. min y 1 ; 4 = − 4
C. min y 1 ; 4 = 4
D. min y 1 ; 4 = 6
Đáp án B
PT hoành độ giao điểm là:
x 3 + 2 x 2 + 5 x + 1 = 3 x + 1 ⇔ x = 0 x 2 + 2 x + 2 = 0 ⇒ x 0 = 0 ⇒ y 0 = 1.
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của hàm số
y
x
+
9
x
trên đoạn
2
;
4
.
A.
min
2
;
4
y
13
2
.
B. ...
Đọc tiếp
Tìm giá trị nhỏ nhất của hàm số y = x + 9 x trên đoạn 2 ; 4 .
A. min 2 ; 4 y = 13 2 .
B. min 2 ; 4 y = 25 4 .
C. min 2 ; 4 y = 6.
D. min 2 ; 4 y = − 6.
Tìm giá trị nhỏ nhất của hàm số y x +
9
x
trên đoạn [2;4]. A.
m
i
n
y
[
2
;
4
]
13
2
B.
m
i
n
...
Đọc tiếp
Tìm giá trị nhỏ nhất của hàm số y = x + 9 x trên đoạn [2;4].
A. m i n y [ 2 ; 4 ] = 13 2
B. m i n y [ 2 ; 4 ] = 25 4
C. m i n y [ 2 ; 4 ] = 6
D. m i n y [ 2 ; 4 ] = -6
Chọn C
Ta có ![]()
Khi đó 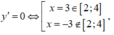
Ta có
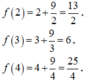
Suy ra: m i n y [ 2 ; 4 ] = 6
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của hàm số y = ( 3x^2 + x + 1) / 3x -2 với x > 2/3
Tìm giá trị nhỏ nhất của hàm số: $y=2x^{2} +\dfrac{5}{x+1}$, $x\ge 2$.
Ta có: \(y-\frac{29}{3}=2x^2+\frac{5}{x+1}-\frac{29}{3}\)
\(=\frac{6x^2\left(x+1\right)+15-29\left(x+1\right)}{3\left(x+1\right)}\)
\(=\frac{6x^3+6x^2+15-29x-29}{3\left(x+1\right)}\)
\(=\frac{6x^3+6x^2-29x-14}{3\left(x+1\right)}\)
\(=\frac{\left(6x^3-12x^2\right)+\left(18x^2-36x\right)+\left(7x-14\right)}{3\left(x+1\right)}\)
\(=\frac{\left(x-2\right)\left(6x^2+18x+7\right)}{3\left(x+1\right)}\ge0\left(\forall x\right)\) vì \(x+1\ge3>0\)
\(\Rightarrow y\ge\frac{29}{3}\)
Dấu "=" xảy ra khi: \(x=2\)
Vậy \(min_y=\frac{29}{3}\Leftrightarrow x=2\)