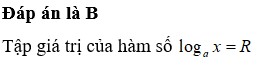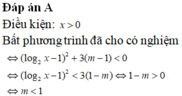Tìm tẩ cả các giá trị của tham số thực để phương trình sin7x=cos2m có nghiệm

Những câu hỏi liên quan
Cho phương trình : cos2x+4cosx+m=0 . Tìm tẩ cả các giá trị tham số m để phương trình đã cho có nghiệm
\(\Leftrightarrow2cos^2x+4cosx-1=-m\)
Xét \(f\left(x\right)=2cos^2x+4cosx-1\)
\(f\left(x\right)=2cos^2x+4cosx+2-3=2\left(cosx+1\right)^2-3\ge-3\)
\(f\left(x\right)=2cos^2x+4cosx-6+5=2\left(cosx-1\right)\left(cosx+3\right)+5\le5\)
\(\Rightarrow-3\le-m\le5\Rightarrow-5\le m\le3\)
Đúng 3
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để phương trình
3
x
m
có nghiệm thực A. m
≥
1
B. m
≥
0
C. m
≠
0
D. m 0
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình 3 x = m có nghiệm thực
A. m ≥ 1
B. m ≥ 0
C. m ≠ 0
D. m > 0
Cho phương trình log 2 m = m với x > 0. Tìm tất cả các giá trị thực của tham số m để phương trình có nghiệm thực
A. m ≥ 0
B. m ∈ R
C. m > 0
D. < 0
Tìm tất cả các giá trị thực của tham số m để phương trình
2
x
m
−
1
có nghiệm thực. A.
m
≥
1
B.
m
≠
1
C. m1 D. m0
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình 2 x = m − 1 có nghiệm thực.
A. m ≥ 1
B. m ≠ 1
C. m>1
D. m>0
Đáp án C
PT có nghiệm thực ⇔ m − 1 > 0 ⇔ m > 1
Đúng 0
Bình luận (0)
Cho phương trình log 2 x = m với x > 0. Tìm tất cả các giá trị thực của tham số m để phương trình có nghiệm thực.
A. m ≥ 0
B. m ∈ ℝ
C. m > 0
D. m ∈ ℤ
Đáp án là B
Tập giá trị của hàm số log a x = R
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số để bất phương trình
log
2
2
x
-
2
log
2
x
+
3
m
-
2
0
có nghiệm thực. A. m 1 B. m
2
3
C. m 0 D. m
≤
1
Đọc tiếp
Tìm tất cả các giá trị thực của tham số để bất phương trình log 2 2 x - 2 log 2 x + 3 m - 2 < 0 có nghiệm thực.
A. m < 1
B. m < 2 3
C. m < 0
D. m ≤ 1
Cho phương trình m 2 x + 6 = 4 x + 3 m . Tìm tất cả các giá trị thực của tham số m để phương trình đã cho có nghiệm.
A. m = 2.
B. m ≠ −2.
C. m ≠ −2 và m ≠ 2.
D. m ∈ R.
Phương trình viết lại m 2 - 4 x = 3 m - 6
Phương trình đã cho vô nghiệm khi m 2 − 4 = 0 3 m − 6 ≠ 0 ⇔ m = ± 2 m ≠ 2 ⇔ m = − 2
Do đó, phương trình đã cho có nghiệm khi m ≠ −2.
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để phương trình
2
x
2
.
5
2
x
+
m
3
có hai nghiệm. A. m log53 + log25 B. m log53 + log25 C. m log23 + log25 D. m log53 + log35
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình 2 x 2 . 5 2 x + m = 3 có hai nghiệm.
A. m < log53 + log25
B. m > log53 + log25
C. m < log23 + log25
D. m > log53 + log35
Chọn A.
Lấy logarit cơ số 2 hai vế của phương trình, ta được ![]()
Hay x2 + (2x + m) log25 - log23 = 0
Nên x2 + 2log25.x + mlog25 - log23 = 0
Để phương trình đã cho có hai nghiệm ![]()
![]()
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số m để phương trình
log
2
4
x
-
1
4
x
+
1
m
có nghiệm thực. A. -1m1 B. m0 C. -1m0 D.
m
≤
-
1
Đọc tiếp
Tìm tất cả các giá trị của tham số m để phương trình log 2 4 x - 1 4 x + 1 = m có nghiệm thực.
A. -1<m<1
B. m<0
C. -1<m<0
D. m ≤ - 1

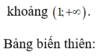
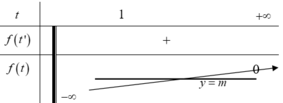
Dựa vào bảng biến thiên để phương trình có nghiệm -> m<0
Đúng 0
Bình luận (0)