Tút gọn rồi tính (theo mẫu):
Mẫu:
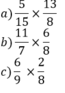
Tính (theo mẫu):
Mẫu
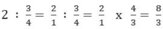
Ta có thể viết gọn như sau: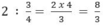
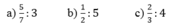
Rút gọn rồi tính (theo mẫu).
| Mẫu: \(\dfrac{5}{15}+\dfrac{4}{3}=\dfrac{1}{3}+\dfrac{4}{3}=\dfrac{1+4}{3}=\dfrac{5}{3}\) |
a) \(\dfrac{21}{15}+\dfrac{2}{5}\) b) \(\dfrac{6}{16}+\dfrac{1}{8}\) c) \(\dfrac{3}{12}+\dfrac{3}{4}\)
a) \(\dfrac{21}{15}\) + \(\dfrac{2}{5}\) = \(\dfrac{9}{5}\)
b) \(\dfrac{6}{16}\) + \(\dfrac{1}{8}\) = \(\dfrac{1}{2}\)
c) \(\dfrac{3}{12}\) + \(\dfrac{3}{4}\) = 1
Tính rồi rút gọn (theo mẫu):
| Mẫu: \(\dfrac{5}{6}+\dfrac{4}{6}=\dfrac{5+4}{6}=\dfrac{9}{6}=\dfrac{3}{2}\) |
a) \(\dfrac{1}{8}+\dfrac{5}{8}\) b) \(\dfrac{1}{15}+\dfrac{4}{15}\) c) \(\dfrac{5}{9}+\dfrac{7}{9}\) d) \(\dfrac{23}{100}+\dfrac{27}{100}\)
a: \(\dfrac{1}{8}+\dfrac{5}{8}=\dfrac{1+5}{8}=\dfrac{6}{8}=\dfrac{3}{4}\)
b: \(\dfrac{1}{15}+\dfrac{4}{15}=\dfrac{1+4}{15}=\dfrac{5}{15}=\dfrac{1}{3}\)
c: \(\dfrac{5}{9}+\dfrac{7}{9}=\dfrac{5+7}{9}=\dfrac{12}{9}=\dfrac{4}{3}\)
d: \(\dfrac{23}{100}+\dfrac{27}{100}=\dfrac{23+27}{100}=\dfrac{50}{100}=\dfrac{1}{2}\)
Tính rồi rút gọn (theo mẫu):
| Mẫu: \(\dfrac{9}{10}-\dfrac{4}{10}=\dfrac{9-4}{10}=\dfrac{5}{10}=\dfrac{1}{2}\) |
a) \(\dfrac{15}{8}-\dfrac{13}{8}\) b) \(\dfrac{7}{15}-\dfrac{2}{15}\) c) \(\dfrac{11}{12}-\dfrac{2}{12}\) d) \(\dfrac{19}{7}-\dfrac{5}{7}\)
a: \(\dfrac{15}{8}-\dfrac{13}{8}=\dfrac{15-13}{8}=\dfrac{2}{8}=\dfrac{1}{4}\)
b: \(\dfrac{7}{15}-\dfrac{2}{15}=\dfrac{7-2}{15}=\dfrac{5}{15}=\dfrac{1}{3}\)
c: \(\dfrac{11}{12}-\dfrac{2}{12}=\dfrac{11-2}{12}=\dfrac{9}{12}=\dfrac{3}{4}\)
d: \(\dfrac{19}{7}-\dfrac{5}{7}=\dfrac{19-5}{7}=\dfrac{14}{7}=2\)
Đặt tính rồi tính (theo mẫu):


Đặt tính rồi tính (theo mẫu):


Đặt tính rồi tính (theo mẫu):


Đặt tính rồi tính (theo mẫu)
Đặt tính rồi tính (theo mẫu):


