Cho tan2a = 4/3 với π/2 < a < π. Giá trị cos a là

Cho π/2 < a < 3π/4. Giá trị tan2a là
A. -2 7 B. 3 3 /4
C. -3 7 D. 3 7
Với π/2 < a < 3π/4 thì cosa < 0. Ta có
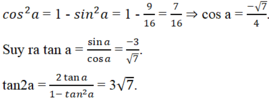
Đáp án là D.
Cho các dòng điện tức thời
i 1 = 5cos(100 π t - π /3)(A)
i 2 = 8cos(100 π t + π /6)(A)
i 3 = 4 2 cos(100 π t - π /4)(A)
Xác định những thời điểm tại đó các cường độ dòng điện trên đây đạt :
- Giá trị cực đại hoặc cực tiểu.
- Giá trị cực đại
- Giá trị 0
Cho sinα=3/5 và 0<α<π/2. Khi đó, giá trị của A= sin(π−α)+cos(π+α)+cos(−α) là gì?
Online chờ gấp, đa tạ các vị!
`A=sin(π-α)+cos(π+α)+cos(-α)`
`= sinα-cosα+cosα=sinα=3/5`
Cho sin a = 3/5 với π/2 < a < π Tính sin 2a , cos 2a , tan 2a , cot ( a - π/4 ) , sin a/2 , cos a/2 Cảm ơn trc❤
Cho sinα = 5 / 4 . Giá trị cos(α + π/2) là
![]()
cos(α+ π/2) = cos(α- π/2+ π) = - cos(α- π/2).
Vậy đáp án là D.
Cho góc α
thỏa mãn `π\2`<α<π,cosα=−\(\dfrac{1}{\sqrt{3}}\). Tính giá trị của các biểu thức sau:
a) sin(α+\(\dfrac{\text{π}}{6}\))
b) cos(α+$\frac{\text{π}}{6}$)
c) sin(α−$\frac{\text{π}}{3}$)
d) cos(α−$\frac{\text{π}}{6}$)
a: pi/2<a<pi
=>sin a>0
\(sina=\sqrt{1-\left(-\dfrac{1}{\sqrt{3}}\right)^2}=\dfrac{\sqrt{2}}{\sqrt{3}}\)
\(sin\left(a+\dfrac{pi}{6}\right)=sina\cdot cos\left(\dfrac{pi}{6}\right)+sin\left(\dfrac{pi}{6}\right)\cdot cosa\)
\(=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{\sqrt{3}}+\dfrac{1}{2}\cdot-\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{6}-2}{2\sqrt{3}}\)
b: \(cos\left(a+\dfrac{pi}{6}\right)=cosa\cdot cos\left(\dfrac{pi}{6}\right)-sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}-\sqrt{2}}{2\sqrt{3}}\)
c: \(sin\left(a-\dfrac{pi}{3}\right)\)
\(=sina\cdot cos\left(\dfrac{pi}{3}\right)-cosa\cdot sin\left(\dfrac{pi}{3}\right)\)
\(=\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}+\dfrac{1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{2}+\sqrt{3}}{2\sqrt{3}}\)
d: \(cos\left(a-\dfrac{pi}{6}\right)\)
\(=cosa\cdot cos\left(\dfrac{pi}{6}\right)+sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}+\sqrt{2}}{2\sqrt{3}}\)
Đặt điện áp xoay chiều có giá trị hiệu dụng U không đổi , f=50 hz vào 2 đầu đoạn mạch gồm điện trở thuần R , cuộn thuần cảm có L thay đổi được , tụ điện có C = \(10^{-4}/ π \) F . Khi L=L1 = \(2/ π \) H thì i=\(I_{1}\sqrt{2}Cos(100 π- π/12)\) . Khi L=L2=4/π thì i=\(I_{2}\sqrt{2}Cos(100 π- π/4)\) . Giá trị của R là
A.\(100\sqrt{3}\)
B.100
C.\(100\sqrt{2}\)
D.200
Tính:F=Cos(π/4+α) x cos(π/4-α)
G=Sin(π/3+α) x cos(π/3-α)
H=cos(π/2-α) x sin(π/2+α)
I=sin(π/4+α) - cos(π/4-α)
K=cos(π/6-x) - sin(π/3+x)