Tìm tập giá trị T của hàm số y = x − 3 + 5 − x .
A. T = 0 ; 2
B. T = 3 ; 5
C. T = 2 ; 2
D. T = 3 ; 5
Tìm tập giá trị T của hàm số y = x - 3 + 5 - x
A. T = (3;5)
B. T = [3;5]
C. T = [ 2 ;2]
D. T = [0; 2 ]
Đáp án C.
Hàm số có tập xác định D = [3;5]
Ta có 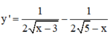
![]()
Suy ra ![]()
Tìm tập giá trị T của hàm số y = x - 3 + 5 - x
A. T = (3;5)
B. T = [3;5]
C. T = 2 ; 2
D. T = 0 ; 2
Tìm tập giá trị T của hàm số y = x - 1 + 9 - x
A.T=[1;9]
B. T = 0 ; 2 2 .
C.T=(1;9)
D. T = 2 2 ; 4 .
Tìm tập giá trị T của hàm số y = x - 1 + 9 - x
A. T = [1;9]
B. T = [0;2 2 ]
C. T = (1;9)
D. T = [2 2 ;4]
Chọn D.
Ta có: TXĐ D = [1;9]
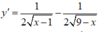
Cho y' = 0 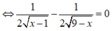
![]()
Ta có: ![]()
Vậy tập giá trị của hàm số là [2 2 ;4]
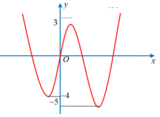
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Biết S là tập các giá trị thực của m để hàm số y = 2 f ( x ) + m có 5 điểm cực trị. Gọi a, b lần lượt là giá trị nguyên âm lớn nhất và giá trị nguyên dương nhỏ nhất của tập S. Tính tổng T = a + b.
A. T = 2
B. T = 1
C. T = -1
D. T = -2
Đáp án A
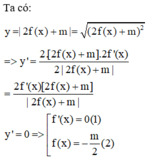
Bài toán cần 5 điểm cực trị => Tổng số nghiệm của (1) và (2) phải là 5
Đối với (1) => số nghiệm chính là số điểm cực trị. Nhìn vào đồ thị => có 3 cực trị
=> Phương trinh (2) phải có 2 nghiệm khác 3 nghiệm trên. Nhìn vào đồ thị ta thấy
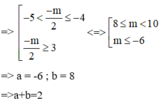
Cho hàm số y=(5-3\(\sqrt{ }\)2)x+\(\sqrt{ }\)2 -1
a) Hàm số đã cho đồng biến hay nghịch biến trên tập?vì sao
b) Tính giá trị của y khi x=5+3\(\sqrt{ }\)2
c) Tìm các giá trị của x khi y=0
a, Vì \(5-3\sqrt{2}>0\) nên hs đồng biến trên R
b, \(x=5+3\sqrt{2}\Leftrightarrow y=25-18+\sqrt{2}-1=6+\sqrt{2}\)
c, \(y=0\Leftrightarrow\left(5-3\sqrt{2}\right)x+\sqrt{2}-1=0\Leftrightarrow x=\dfrac{1-\sqrt{2}}{5-3\sqrt{2}}\)
\(\Leftrightarrow x=\dfrac{\left(1-\sqrt{2}\right)\left(5+3\sqrt{2}\right)}{7}=\dfrac{-2\sqrt{2}-1}{7}\)
Cho hàm số y = f(x) có đồ thị như hình bên. Biết S là tập các giá trị thực của m để hàm số y = 2 f x + m có 5 điểm cực trị. Gọi a, b lần lượt là giá trị nguyên âm lớn nhất và giá trị nguyên dương nhỏ nhất của tập S. Tổng T=a+b là
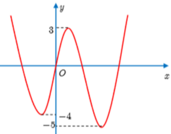
A. 2
B. 1
C. -1
D. 3
Cho hàm số g ( x ) = ∫ x x 2 d t ln t với x>1. Tìm tập giá trị T của hàm số
![]()
![]()
![]()
![]()
Cho hàm số g x = ∫ x x 2 d t ln t với x > 1. Tìm tập giá trị T của hàm số
A. T = 0 ; + ∞
B. T = [ 1 ; + ∞ )
C. T = - ∞ ; ln 2
D. T = ln 2 ; + ∞
Ta có g ' x = 2 x 1 ln x 2 - 1 ln x = x - 1 ln > 0 , ∀ x > 1 ⇒ g(x) đồng biến trên 1 ; + ∞
Suy ra tập giá trị của hàm số g(x) là T = g 1 + ; g + ∞
Do 1 ln t là hàm số nghịch biến nên g x ≥ x 2 - x 1 ln x 2 → + ∞ khi x → + ∞
Do đó g + ∞ = + ∞
Để tính g 1 + đặt t = e x , ta được g x = ∫ ln x 2 ln x e v v d v
Khi đó g x < e 2 ln x = ∫ ln x 2 ln x d v v = x 2 ln 2
Chứng minh tương tự, ta thu được g(x) > xln(2)
Theo định lí kẹp, ta suy ra g 1 + = ln 2
Vậy tập giá trị của hàm số đã cho là T = ln 2 ; + ∞
Đáp án D