Chọn D.
Ta có: TXĐ D = [1;9]
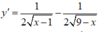
Cho y' = 0 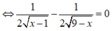
![]()
Ta có: ![]()
Vậy tập giá trị của hàm số là [2 2 ;4]
Chọn D.
Ta có: TXĐ D = [1;9]
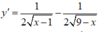
Cho y' = 0 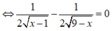
![]()
Ta có: ![]()
Vậy tập giá trị của hàm số là [2 2 ;4]
Gọi S là tập hợp tất cả các giá trị nguyên dương và nhỏ hơn 2018 của tham số m để hàm số y = x - 2 x - m nghịch biến trên khoảng (1;9). Tính số phần tử của tập hợp S.
![]()
![]()
![]()
![]()
Cho hàm số g ( x ) = ∫ x x 2 d t ln t với x>1. Tìm tập giá trị T của hàm số
![]()
![]()
![]()
![]()
Tìm tập hợp T tất cả các giá trị của tham số m để hàm số y = x 3 - 2 mx 2 + m 2 x + 1 đạt cực tiểu tại x= 1
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số y = 2 x - m x + 2 với m là tham số , m ≠ 4 . Tìm giá trị của tham số m thỏa mãn min f ( x ) x ∈ [ 0 ; 2 ] + m a x f ( x ) x ∈ [ 0 ; 2 ] = - 8
A. m= 8
B. m= 9
C. m= -12
D. m= 10
Gọi M,m là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 2 - 1 x - 2 trên tập hợp D = ( - ∞ ; - 1 ] ∪ 1 ; 3 2 Khi đó T = m.M bằng
A. 1 9
B. 0
C. 3 2
D. - 3 2
Cho hàm số f ( x ) = ∫ 1 x d t t 2 + t ( x > 1 ) Tập giá trị của hàm số là:
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-1)²+y²+ (z+2)²=4 và đường thẳng d : x = 2 - y y = t z = m - 1 + t . Gọi T là tập tất cả các giá trị của m để d cắt (S) tại hai điểm phân biệt A, B sao cho các tiếp diện của (S) tại A và B tạo với nhau góc lớn nhất có thể. Tính tổng các phần tử của tập hợp T.
A. 3
B. -3
C. -5.
D. -4.
Tìm giá trị lớn nhất của hàm số y = f ( x ) = x 3 - 2 x 2 + x - 2 trên đoạn [0;2]
A. ![]()
B. 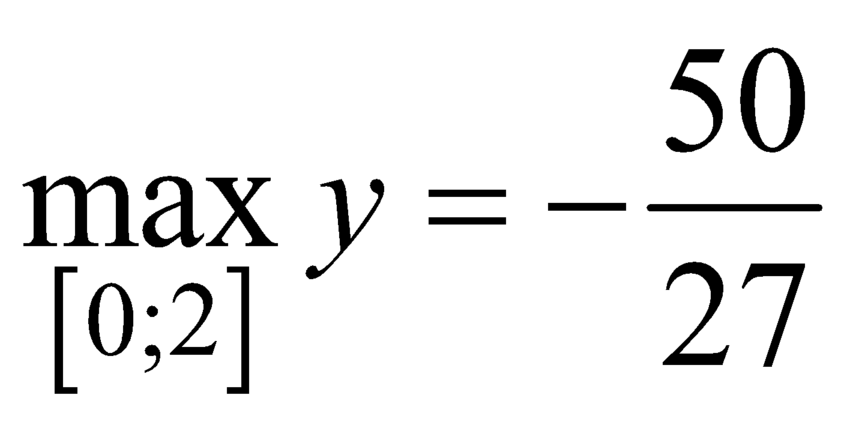
C. ![]()
D. ![]()
Đồ thị hàm số y = 1 - 2 x 2 x 2 + 6 x + 9 có tiệm cận đứng x = a và tiệm cận ngang y = b. Tính giá trị T = 2 a - b
A. T = -4
B. T = -8
C. T = -1
D. T = -6