Cho f x = x . e − 3 x , tập nghiệm của bất phương trình f ' x > 0 là
A. (0;1)
B. 0 , 1 3 .
C. − ∞ , 1 3 .
D. 1 3 , + ∞ .
Những câu hỏi liên quan
Cho hàm số
f
(
x
)
l
n
(
x
2
-
2
x
+
3
)
. Tập nghiệm của bất phương trình f(x)0 là A.
(
2
;
+
∞
)
. B.
(
-
1
;
+
∞
)
. C.
(
-
2
;
+
∞
)...
Đọc tiếp
Cho hàm số f ( x ) = l n ( x 2 - 2 x + 3 ) . Tập nghiệm của bất phương trình f'(x)>0 là
A. ( 2 ; + ∞ ) .
B. ( - 1 ; + ∞ ) .
C. ( - 2 ; + ∞ ) .
D. ( 1 ; + ∞ ) .
Cho tập số f ( x ) = x - 2 x 2 + 12 Tập nghiệm của bất phương trình f'(x)≤0 là:
A. (-∞;2)∪[2;+∞)
B. (-∞;2)
C. [2;+∞)
D. (2;+∞)
Cho hàm số y f(x) có bảng biến thiên như hình vẽ bên và f(-2) 3. Tập nghiệm của bất phương trình f(x) 3 là A.
S
-
2
;
2
B.
S
-
∞
;
-
2
C.
S
-
∞
;
-...
Đọc tiếp
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ bên và f(-2) = 3. Tập nghiệm của bất phương trình f(x) > 3 là
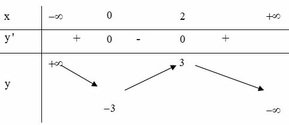
A. S = - 2 ; 2
B. S = - ∞ ; - 2
C. S = - ∞ ; - 2 ∪ 2 ; + ∞
D. S = - 2 ; + ∞
Cho
f
(
x
)
x
.
e
-
3
x
, tập nghiệm của bất phương trình
f
(
x
)
0
là
Đọc tiếp
Cho f ( x ) = x . e - 3 x , tập nghiệm của bất phương trình f ' ( x ) > 0 là
SGK Kết nối tri thức và cuộc sống
17 tháng 8 2023 lúc 16:57
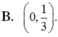
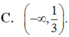
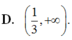
Cho hàm số \(f(x) = \frac{1}{3}{x^3} - {x^2} - 3x + 1\). Tập nghiệm của bất phương trình \(f'(x) \le 0\) là
A. [1 ; 3].
B. \([ - 1;3]\).
C. \([ - 3;1]\).
D. \([ - 3; - 1]\)
Ta có: \(f'\left(x\right)=x^2-2x-3\)
\(f'\left(x\right)\le0\\ \Rightarrow x^2-2x-3\le0\\ \Leftrightarrow\left(x+1\right)\left(x-3\right)\le0\\ \Leftrightarrow-1\le x\le3\)
Đúng 0
Bình luận (0)
Cho
f
(
x
)
1
2
.
5
2
x
+
1
;
g
(
x
)
5
x
+
4
x
.
ln
5
.
Tập nghiệm của bất phương trình
f
(
x
)...
Đọc tiếp
Cho f ( x ) = 1 2 . 5 2 x + 1 ; g ( x ) = 5 x + 4 x . ln 5 . Tập nghiệm của bất phương trình f ' ( x ) > g ' ( x ) là
A. x>1.
B. x>0.
C. 0<x<1.
D. x<0.
Cho
f
(
x
)
1
2
.
5
2
x
+
1
;
g
(
x
)
5
x
+
4
x
.
ln
5
.
Tập nghiệm của bất phương trình
f
(
x
)...
Đọc tiếp
Cho f ( x ) = 1 2 . 5 2 x + 1 ; g ( x ) = 5 x + 4 x . ln 5 . Tập nghiệm của bất phương trình f ' ( x ) > g ' ( x ) là
A. x>1.
B. x>0.
C. 0<x<1.
D. x<0.
Cho hàm số f(x) log2(x - 1). Tìm tập nghiệm của bất phương trình f(x + 1) 1. A. x 2 B. x 4 C. x 1 D. 1 x 2
Đọc tiếp
Cho hàm số f(x) = log2(x - 1). Tìm tập nghiệm của bất phương trình f(x + 1) > 1.
A. x > 2
B. x < 4
C. x > 1
D. 1 < x < 2
Chọn A.
Ta có: f(x + 1) = log2x
Khi đó f(x + 1) > 1 khi và chỉ khi log2x > 1 hay x > 2.
Đúng 0
Bình luận (0)
Tập nghiệm của bất phương trình
f
(
x
)
x
-
1
x
2
+
4
x
+
3
≤
0
A.
S
-
∞
;...
Đọc tiếp
Tập nghiệm của bất phương trình f ( x ) = x - 1 x 2 + 4 x + 3 ≤ 0
A. S = - ∞ ; 1
B. 
C. 
D. 
Chọn C
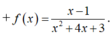
Ta có x-1=0 khi x= 1 và x 2+ 4x+3= 0 khi và chỉ khi x= -3 hoặc x= -1
+ Lập bảng xét dấu f(x) :
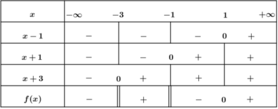
+ Vậy f(x) ≤ 0 khi 
Vậy 
Đúng 0
Bình luận (0)
cho f(x)=\(\frac{x^3}{3}+\frac{x^2}{2}+x\)
Tập nghiệm của bất phương trình f'(x)\(\le\)0 là
\(f'\left(x\right)=x^2+x+1\) luôn lớn hơn 0 mà :3 vậy f'(x) \(\le\)0 là k có :3
Đúng 0
Bình luận (2)