Chọn A.
Ta có: f(x + 1) = log2x
Khi đó f(x + 1) > 1 khi và chỉ khi log2x > 1 hay x > 2.
Chọn A.
Ta có: f(x + 1) = log2x
Khi đó f(x + 1) > 1 khi và chỉ khi log2x > 1 hay x > 2.
Cho hàm số f(x) = log2x và g(x) = log2(4-x) . Tìm tập nghiệm của bất phương trình f(x + 1) < g(x + 2)
A. S = - ∞ ; 1 2
B. S = - 1 ; 1 2
C. S = (0; 2).
D. S = - ∞ ; 2
Cho hàm số y = f ( x ) = ln ( 1 + x 2 + x ) .
Tập nghiệm của bất phương trình
f ( a - 1 ) + f ( ln a ) ≤ 0 là:
![]()
![]()
![]()
![]()
Nghiệm của bất phương trình log 2 ( 3 x - 2 ) < 0 là:
A. x > 1 B. x < 1
C. 0 < x < 1 D. log 3 2 < x < 1
Tìm tập hợp nghiệm của phương trình log 2 + log 2 ( x - 1 ) = 1
A. {1} B. {2}
C. {1;2} D. {-1;2}
Cho hàm số f(x) = 1 3 x 3 + x 2 - 3 x + 1 . Tìm nghiệm của bất phương trình f ' ( x ) ≤ 0
![]()
![]()
![]()
![]()
Gọi S1 là tập nghiệm của bất phương trình log 2 ( x + 5 ) + log 1 2 ( 3 - x ) ≥ 0 và S2 là tập nghiệm của bất phương trình log2(x + 1) ≥ 1. Khẳng định nào dưới đây đúng ?
A. S 1 ∩ S 2 = [ 1 ; 3 )
B. S 1 ∩ S 2 = [ - 1 ; 3 )
C. S 1 ∩ S 2 = - 1 ; 1
D. S 1 ∩ S 2 = 1 ; 3
Tìm số nghiệm nguyên của bất phương trình log 5 2 ( 3 x - 2 ) log 2 ( 4 - x ) - log ( 4 - x ) 2 + 1 > 0
A. 3
B. 1
C. 0
D. 2
Cho F(x) là một nguyên hàm của hàm số 1 e x + 1 , thỏa mãn F(0) = –ln2. Tìm tập nghiệm S của phương trình F(x) + ln(ex + 1) = 3.
A. S = 3
B. S = - 3
C. S = ∅
D. S = ± 3
Cho hàm số y=f(x) có đạo hàm trên ℝ . Đồ thị của hàm số y=f'(x) như hình dưới
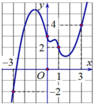
Tìm m để bất phương trình m + x 2 + 4 ≥ 2 f x + 1 - 2 x nghiệm đúng với mọi x ∈ - 4 ; 2
A. m ≥ 2 f ( 0 ) - 1
B. m ≥ 2 f ( - 3 ) - 4
C. m ≥ 2 f ( 3 ) - 16
D. m ≥ 2 f ( 1 ) - 4