A

BPT đã cho vô nghiệm khi:

\(\left\{{}\begin{matrix}m^2-4=0\\m+2\le0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=\pm2\\m\le-2\end{matrix}\right.\) \(\Rightarrow m=-2\)

B đúng

Rõ ràng nếu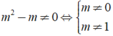

thì bất phương trình luôn có nghiệm.

Với m = 0, bất phương trình trở thành 0x < 0: vô nghiệm.

Với m = 1, bất phương trình trở thành 0x < 1: luôn đúng với mọi x ∈ R

Vậy với m = 0 thì bất phương trình trên vô nghiệm.

Rõ ràng nếu m 2 - m ≠ 0  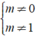⇔ thì bất phương trình luôn có nghiệm.

Với m = 0, bất phương trình trở thành 0x < 0: vô nghiệm.

Với m = 1, bất phương trình trở thành 0x < 1: luôn đúng với mọi x ∈ R

Vậy với m = 0 thì bất phương trình trên vô nghiệm.

Đáp án B.

Phương pháp: 

Bất phương trình m ≥ f x ,    x ∈ D có nghiệm khi và chỉ khi m ≥ M i n D f x .  

Cách giải:

ĐKXĐ:  0 < x < 1

3 log x ≤ 2 log m x − x 2 − 1 − x 1 − x ⇔ m x − x 2 − 1 − x 1 − x ≥ x x

⇔ m ≥ x x + 1 − x 1 − x x − x 2 ,    x ∈ 0 ; 1

Để bất phương trình đã cho có nghiệm thực thì m ≥ M i n 0 ; 1 f x , f x = x x + 1 − x 1 − x x − x 2  

Xét

f x = x x + 1 − x 1 − x x − x 2 = x + 1 − x 1 − x x − 1 x x − 1 , x ∈ 0 ; 1  

Đặt t = x + 1 − x ,    t ∈ 1 ; 2  

Khi đó,  

f x = x + 1 − x 1 − x 1 − x x 1 − x = t 1 − t 2 − 1 2 t 2 − 1 2 = t 3 − t 2 t 2 − 1 = 3 t − t 3 t 2 − 1 = g t

g ' t = − t 4 − 3 t 2 − 1 2 < 0 ,     ∀ t ∈ 1 ; 2  

⇒ g t min = g 2 = 3 2 − 2 2 2 − 1 = 2 ⇒ M i n 0 ; 1 f x = 2 ⇒ m ≥ 2  

Mà

m ∈ − 9 ; 9 ⇒ m ∈ 2 ; 3 ; 4 ; ... ; 8 ⇒

Có 7 giá trị thỏa mãn.

Đáp án B

Đáp án A.

\(mx^2-2\left(m+2\right)x+2m-1< 0\)

\(< =>mx^2-2\left(m+2\right)x+2m-1\ge0\)

\(a=m\ne0\)

\(\Delta=\left(2m+2\right)^2-4m\left(2m-1\right)\)

\(\Delta=4m^2+8m+4-8m^2+4m\)

\(\Delta=12m-4m^2+4\)

\(< =>\hept{\begin{cases}a>0\\\Delta\le0\end{cases}\hept{\begin{cases}m>0\\12m-4m^2+4\le0\end{cases}\hept{\begin{cases}m>0\\m=\left[\frac{3-\sqrt{13}}{2};\frac{3+\sqrt{13}}{2}\right]\end{cases}}}}\)

\(< =>m=(0;\frac{3+\sqrt{13}}{2}]\)

vậy m vô số nghiệm để bpt vô nghiệm