Rõ ràng nếu
m
2
-
m
≠
0
⇔ 
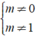thì bất phương trình luôn có nghiệm.
Với m = 0, bất phương trình trở thành 0x < 0: vô nghiệm.
Với m = 1, bất phương trình trở thành 0x < 1: luôn đúng với mọi x ∈ R
Vậy với m = 0 thì bất phương trình trên vô nghiệm.
Có bao nhiêu giá trị thực của tham số m để bất phương trình m 2 - m x < m vô nghiệm là?
Cho phương trình: ( - m 2 – m + 2)x = m + 2, với m là tham số. Giá trị của m để phương trình vô số nghiệm là:
A. m = 1
B. m = 2
C. m = -2
D. m Є {1; 2}
Tìm tất cả các giá trị của tham số m để bất phương trình m( x - 1 ) < 3 - x có nghiệm?
A. m ≠ 1
B. m = 1
C. m ∈ R
D. m ≠ 3
Tìm các giá trị của tham số m để mọi giá trị của x nhỏ hơn \(\dfrac{-1}{2}\) đều là nghiệm của bất phương trình (2m + 3).(x - m) > 4x - 3 + 2m
1. Xác định giá trị của m để phương trình (m + 7)x = 2m – 1 vô nghiệm.
2. Giải phương trình (với m là tham số) : (m – 2)x = m – 2.
(giúp mình với)
Cho bất phương trình:
3(m -1) +x > 2m
a) Tìm giá trị của m để bất phương trình vô nghiệm
b) Tìm m để mọi giá trị của x > 1 đều là nghiệm của bất phương trình
Tìm tất cả các giá trị của tham số m để bất phương trình m 2 + m - 6 x ≥ m + 1 có nghiệm?
A. m ≠ 2
B. m ≠ 2, m ≠ 3
C. m ∈ R
D. m ≠ 3
Với giá trị nào của m và n thì bất phương trình sau có vô số nghiệm? (m-2n+1)x>m^2+n^2-2
cho phương trình (m2-9)x=m2-2m-3(m là tham số)
a. tìm m để phương trình có một nghiệm duy nhất. tìm nghiệm đó.
b. tìm m để phương trình vô nghiệm
c. tìm m để phương trình vô số nghiệm.
