Rõ ràng: m 2 + m - 6 ≠ 0 thì bất phương trình luôn có nghiệm
Xét m 2 + m - 6 = 0
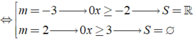
Từ hai trường hợp, ta được bất phương trình có nghiệm khi m ≠ 2
Chọn đáp án A.
Rõ ràng: m 2 + m - 6 ≠ 0 thì bất phương trình luôn có nghiệm
Xét m 2 + m - 6 = 0
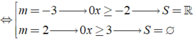
Từ hai trường hợp, ta được bất phương trình có nghiệm khi m ≠ 2
Chọn đáp án A.
Tìm tất cả các giá trị của tham số m để bất phương trình m( x - 1 ) < 3 - x có nghiệm?
A. m ≠ 1
B. m = 1
C. m ∈ R
D. m ≠ 3
Tìm các giá trị của tham số m để mọi giá trị của x nhỏ hơn \(\dfrac{-1}{2}\) đều là nghiệm của bất phương trình (2m + 3).(x - m) > 4x - 3 + 2m
1) Giải phương trình: \(\left(2021x-2020\right)^3=8\left(x-1\right)^3+\left(2019x-2018\right)^3\)
2) Cho phương trình ẩn x: \(x\left(2x-3\right)+x\left(x-m\right)=3x^2+x-m\) , với m là tham số. Tìm tất cả các giá trị của tham số m để phương trình có nghiệm không âm.
cho PT ẩn x (m là tham số): (m+3)/(x+1) - (5- 3m)/(x- 2) = (mx +3)/(x2- x- 2)
tìm tất cả các giá trị của tham số m để phương trình này vô nghiệm
p/s tra loi nhanh giup minh, ai nhanh nhat minh tick cho
Cho phương trình\(\left(m^2+2m+3\right)\cdot\left(x-6\right)=0.\)
(m là tham số)
a) Tìm giá trị của m để phương trình nhận x=2 là một nghiệm
b) Tìm giá trị của m để phương trình có nghiệm x duy nhất đạt giá trị lớn nhất
Cho phương trình: m2x + m(x - 3) = 6(x - 1) (m là tham số) (1)
a. Giải phương trình (1) khi m = 1
b. Tìm m để phương trình (1) có một nghiệm duy nhất thỏa mãn biểu thức A=x^2+2x+3/x^2+2 đạt giá trị nhỏ nhất?
Cho phương trình: m2x + m(x - 3) = 6(x - 1) (m là tham số) (1)
a. Giải phương trình (1) khi m = 1
b. Tìm m để phương trình (1) có một nghiệm duy nhất thỏa mãn biểu thức A=x^2+2x+3/x^2+2 đạt giá trị nhỏ nhất?
Giải và biện luận các phương trình sau (với m là tham số):
a) mx – x – m + 2 = 0
\(b) m^2x + 3mx – m^2 + 9 = 0 \)
\(c) m^3x – m^2 - 4 = 4m(x – 1)\)
2) Cho phương trình ẩn x: . Hãy xác định các giá trị của k để phương trình trên có nghiệm x = 2.
Tìm giá trị của m để 2 bất phương trình sau có đúng 1 nghiệm chung
m (m + 3) ≤ x + 5 và m (x + 2) - 3 ≥ x