Cho hàm số f(x) thỏa mãn f x + 2 x f ' x = 3 x e − x , ∀ x ∈ [ 0 ; + ∞ ) . Giá trị f(1) bằng
A. 1 + 1 e .
B. 2 e
C. 1 e
D. 1 + 2 e .
Cho hàm số y=f(x) xác định và liên tục trên [1;e] thỏa mãn xf ' ( x ) = x [ f ( x ) ] 2 + 3 f ( x ) + 4 x và f(1) = -3. Tính f(e).
A. 5 2 e
B. - 5 2
C. - 5 2 e
D. 5 2
Tìm nguyên hàm F(x) của hàm số f ( x ) = 3 x 2 − e − x thỏa mãn F ( 0 ) = 3 .
A. F ( x ) = x 3 − e − x − 3
B. F ( x ) = x 3 + e − x + 2
C. F ( x ) = x 3 − e − x + 3
D. F ( x ) = x 3 + e − x − 2
Tìm nguyên hàm F(x) của hàm số f ( x ) = 3 x 2 - e - x thỏa mãn F(0)=3
![]()
![]()
![]()
![]()
Cho hàm số y=f(x) thỏa mãn f ' ( x ) + 2 x f ( x ) = e - x 2 , ∀ x ∈ R và f(1)=0 Tính giá trị f(2).
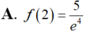
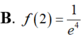
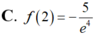
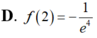
Cho hàm số F ( x ) = a x 3 + b x 2 + c x + 1 là một nguyên hàm của hàm số f(x) thỏa mãn f(1) = 2, f(2) = 3, f(3) = 4. Hàm số F(x) là
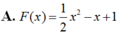
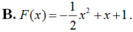
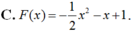
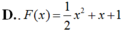
Cho hàm số f(x) thỏa mãn 2.f(1/x)+f(x)= x^2. Tính f(3)
Cho hàm số f(x) thỏa mãn: xf'(x).lnx + f(x) = 2x2, ∀x ∈ (1;+∞) và f(e) = e2. Tính tích phân I=\(\int\limits^{e^2}_e\dfrac{x}{f\left(x\right)}dx\)
Cách làm cơ bản của dạng này:
Cho F(x) là một nguyên hàm của hàm số f ( x ) = e x + 2 x thỏa mãn F(0)=3/2. Tìm F(x)
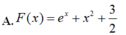
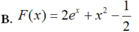
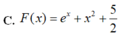
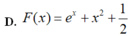
Cho F(x) là một nguyên hàm của hàm số f(x)=|1+x|-|1-x| trên tập R và thỏa mãn F(1)= 3.Tính tổng F(0)+F(2)+F(-3).
![]()
![]()
![]()
![]()
Cho hàm số f(x) thỏa mãn f x + f ' x = e - x , ∀ x ∈ ℝ và f(0) = 2. Tất cả các nguyên hàm của f x e 2 x là
A. x - 2 e x + e x + C
B. x + 2 e x + e x + C
C. x - 1 e x + C
D. x + 1 e x + C