Cho hình hộp đứng ABCD. A 1 B 1 C 1 D 1 có đáy ABCD là hình vuông cạnh a, đường thẳng D B 1 tạo với mặt phẳng (x D B 1 ) góc 30°. Tính thể tích khối hộp ABCD. A 1 B 1 C 1 D 1
A. a 3 3
B. a 3 2
C. a 3
D. a 3 2 3
Những câu hỏi liên quan
Cho hình hôp đứng ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a và góc BAD=60.Biết AB' hợp với mặt đáy(ABCD) 1 góc 30.Tính thể tích khối hộp
\(\Delta ABD\) đều cạnh a.
\(\Rightarrow S_{ABD}=\frac{a^2\sqrt{3}}{4}\Rightarrow S_{ABCD}=2S_{ABD}=\frac{a^2\sqrt{3}}{2}\)
\(\Delta ABB'\)vuông tại B \(\Rightarrow BB'=AB\tan30^o=a\sqrt{3}V=B.h=S_{ABCD}.BB'=\frac{3a^3}{2}\)
Đúng 0
Bình luận (6)
Cho hình Chóp S.ABC có mặt bên SBC là tam giác đều cạnh a , cạnh bên SA vuông góc với đáy . Biết góc BAC = 120 độ . Tính thể tích khối Chóp
Đúng 0
Bình luận (0)
1.Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi A',B' lần lượt là trung điểm của SA,SB . Đường thẳng A' B' song song với mặt phẳng nào dưới đây?
A. (SAB).
B. ( ABCD) .
C. (SAD).
D. (SBC).
2.Cho hình hộp ABCD.A' B' C' D' . Mặt phẳng ( ABA') song song với:
A. ( AA'C') .
B. (CC'D').
C. ( ADD').
D. (BB'A').
Hình hộp đứng ABCD.A′B′C′D′ có đáy là hình thoi. Diện tích các tứ giác ABCD,ACC′A′,BDD′B′ lần lượt là
S
1
,
S
2
,
S
3
.
Khi đó thể tích khối hộp ABCD.A′B′C′D′ là A.
1
3
S
1
S
2...
Đọc tiếp
Hình hộp đứng ABCD.A′B′C′D′ có đáy là hình thoi. Diện tích các tứ giác ABCD,ACC′A′,BDD′B′ lần lượt là S 1 , S 2 , S 3 . Khi đó thể tích khối hộp ABCD.A′B′C′D′ là
A. 1 3 S 1 S 2 S 3
B. 1 2 S 1 S 2 S 3
C. 1 3 S 1 S 2 S 3
D. 1 2 S 1 S 2 S 3
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a và
B
A
D
^
60
0
, hợp với đáy (ABCD) một góc
30
0
. Thể tích của khối hộp là
Đọc tiếp
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a và B A D ^ = 60 0 , hợp với đáy (ABCD) một góc 30 0 . Thể tích của khối hộp là
Cho hình hộp đứng ABCD.ABCD có đáy ABCD là hình thoi cạnh a và
B
A
D
^
60
0
,
A
B
hợp với đáy (ABCD) một góc
30
°
. Thể tích của khối hộp là A.
a...
Đọc tiếp
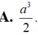
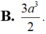
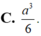
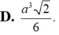
Cho hình hộp đứng ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a và B A D ^ = 60 0 , A B ' hợp với đáy (ABCD) một góc 30 ° . Thể tích của khối hộp là
A. a 3 2 .
B. 3 a 3 2 .
C. a 3 6 .
D. a 3 2 6 .
Cho hình hộp đứng ABCD.ABCD có đáy ABCD là hình thoi cạnh a và
B
A
D
^
60
0
, AB hợp với đáy (ABCD) một góc
30
0
. Thể tích của khối hộp là A.
a
3
2
B.
3
a...
Đọc tiếp
Cho hình hộp đứng ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a và B A D ^ = 60 0 , AB' hợp với đáy (ABCD) một góc 30 0 . Thể tích của khối hộp là
A. a 3 2
B. 3 a 3 2
C. a 3 6
D. a 3 2 6
Đáp án C
B D = a ⇒ B O = a 2 ⇒ A O = a 2 - a 2 4 = a 3 2 ⇒ A C = a 3 A ' A , A B C D = A ' A , A ' B ' = A B ' A ' ⇒ A A ' = A ' B ' . tan 30 0 = a 3 3 ⇒ V = 1 3 a 3 3 1 2 a 3 . a = a 3 6
Đúng 0
Bình luận (0)
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a và
B
A
D
^
60
0
,
AB’ hợp với đáy (ABCD) một góc
30
0
.
Thể tích của khối hộp là A.
a
3
2
.
B.
3...
Đọc tiếp
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a và B A D ^ = 60 0 , AB’ hợp với đáy (ABCD) một góc 30 0 . Thể tích của khối hộp là
A. a 3 2 .
B. 3 a 3 2 .
C. a 3 6 .
D. a 3 2 6 .
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a và
B
D
C
⏜
60
0
, AB’ hợp với đáy (ABCD) một góc
30
0
. Thể tích của khối hộp là
Đọc tiếp
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a và B D C ⏜ = 60 0 , AB’ hợp với đáy (ABCD) một góc 30 0 . Thể tích của khối hộp là
SGK Chân trời sáng tạo
20 tháng 8 2023 lúc 21:40
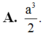
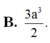
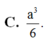
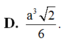
Cho hình hộp đứng \(ABCD.A'B'C'D'\) có cạnh bên \(AA' = 2a\) và đáy \(ABCD\) là hình thoi có \(AB = a\) và \(AC = a\sqrt 3 \).
a) Tính khoảng cách giữa hai đường thẳng \(B{\rm{D}}\) và \(AA'\).
b) Tính thể tích của khối hộp.
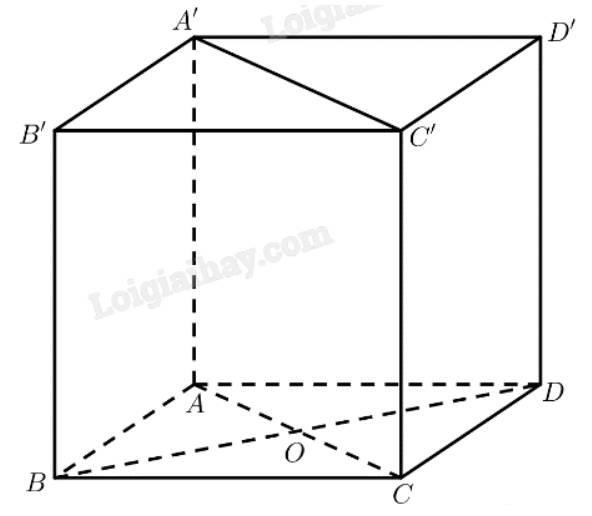
a) Gọi \(O = AC \cap B{\rm{D}}\)
\(ABCD\) là hình thoi \( \Rightarrow AC \bot B{\rm{D}} \Rightarrow AO \bot B{\rm{D}}\)
\(AA' \bot \left( {ABCD} \right) \Rightarrow AA' \bot AO\)
\( \Rightarrow d\left( {B{\rm{D}},AA'} \right) = AO = \frac{1}{2}AC = \frac{{a\sqrt 3 }}{2}\)
b) Tam giác \(OAB\) vuông tại \(O\)
\(\begin{array}{l} \Rightarrow BO = \sqrt {A{B^2} - A{O^2}} = \frac{a}{2} \Rightarrow B{\rm{D}} = 2BO = a\\{S_{ABC{\rm{D}}}} = \frac{1}{2}AC.B{\rm{D}} = \frac{{{a^2}\sqrt 3 }}{2}\\{V_{ABC.A'B'C'}} = {S_{ABC{\rm{D}}}}.AA' = \frac{{3{a^3}}}{4}\end{array}\)
Đúng 0
Bình luận (0)