Đáp án B

Th1 : Số cách chọn ra 1 nhà toán học nam, 1 nhà toán học nữ, 1 nhà vật lý nam : 5.3.4 = 60

Th2 : Số cách chọn ra 2 nhà toán học nữ, 1 nhà vật lý nam :  C 3 2 . C 4 1 = 12

Th3 : Số cách chọn ra 1 nhà toán học nữ, 2 nhà vật lý nam :  C 3 1 C 4 2 = 18

Vậy có số cách chọn là : 90.

Đáp án A.  

* Hướng dẫn giải:

+ Đoàn công tác gồm: 1 nhà toán học nữ, 1 nhà vật lý và 1 nhà toán học nam 

   Số các để chọn: cách

+ Đoàn công tác gồm: 1 nhà toán học nữ, 2 nhà vật lý

   Số cách chọn: cách

+ Đoàn công tác gồm: 2 nhà toán học nữ, 1 nhà vật lý

   Số cách chọn: cách

Vậy số cách lập là: 210 cách

Ta có các khả năng sau

 Đoàn công tác gồm: 1 nhà toán học nữ, 1 nhà vật lý và 1 nhà toán học nam

Số cách chọn:  cách

 Đoàn công tác gồm: 1 nhà toán học nữ, 2 nhà vật lý

Số cách chọn:  cách

 Đoàn công tác gồm: 2 nhà toán học nữ, 1 nhà vật lý

Số cách chọn:  cách

Vậy số cách lập là: 210 cách.

Chọn A.

Ta có các khả năng sau

- Đoàn công tác gồm: 1 nhà toán học nữ, 1 nhà vật lý và 1 nhà toán học nam

Số cách chọn: C 7 1 . C 4 1 . C 5 1 = 140  cách

- Đoàn công tác gồm: 1 nhà toán học nữ, 2 nhà vật lý

Số cách chọn: C 4 1 . C 5 2 = 40  cách

- Đoàn công tác gồm: 2 nhà toán học nữ, 1 nhà vật lý

Số cách chọn: C 4 2 . C 5 1 = 30  cách

Vậy số cách lập là: 140 + 40 + 30 = 210  cách.

Chọn đáp án A.

có 5 cách nha bạn

th1: chọn 1 nhà toán học nam, 1 nhà toán học nữ, 1 nhà vật lý nam

có: 5.3.4 = 60 (cách chọn)

th2: chọn 2 nhà toán học nữ, 1 nhà vật lý nam

có: 3C2.4C1 = 12 (cách chọn)

th3: chọn 1 nhà toán học nữ, 2 nhà vật lý nam

có: 3C1.4C2 = 18 (cách chọn)

vậy có tổng cộng 60 + 12 + 18 = 90 cách chọn

có 5 cách nha

a.

Chọn 1 nam từ 9 nam có 9 cách

Chọn 1 nữ từ 3 nữ có 3 cách

\(\Rightarrow\) Có \(9.3=27\) cách chọn nhóm 1 nam 1 nữ

b.

Chọn 2 nhà toán học từ 8 nahf toán học: \(C_8^2\) cách

Chọn 2 nhà vật lý từ 4 nhà vật lý: \(C_4^2\) cách

\(\Rightarrow C_8^2.C_4^2\) cách lập

c.

Các trường hợp thỏa mãn: (1 nhà toán học nữ, 2 nhà vật lý nam), (1 nhà toán học nữ, 1 nhà toán học nam, 1 nhà vật lý nam), (2 nhà toán học nữ, 1 nhà vật lý nam)

\(\Rightarrow C_3^1.C_4^2+C_3^1.C_5^1.C_4^1+C_3^2.C_4^1\) cách

Chọn C.

Số cách chọn 4 nhà khoa học mà có đủ cả ba lĩnh vực là 

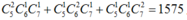
Số cách chọn 4 nhà khoa học nam mà có đủ cả ba lĩnh vực là 

Số cách chọn 4 nhà khoa học nữ mà có đủ cả ba lĩnh vực là 

Vậy số cách lập một ban thư kĩ thỏa mãn yêu cầu là:

Đáp án B.

Số cách chọn 5 em học sinh từ 8 học sinh trên là cách

- Để chọn 5 em thỏa mãn bài ra, ta xét các trường hợp sau

+) 1 nam khối 11, 1 nữ khối 12 và 3 nam khối 12 có cách

+) 1 nam khối 11, 2 nữ khối 12 và 2 nam khối 12 có cách

+) 2 nam khối 11, 1 nữ khối 12 và 2 nam khối 12 có cách

+) 2 nam khối 11, 2 nữ khối 12 và 1 nam khối 12 có cách

- Số cách chọn 5 em thỏa mãn bài ra là:

cách

Vậy xác suất cần tính là: