Biết đồ thị của hàm số y = x 4 - 2 m x 2 + 1 có ba điểm cực trị A 0 ; 1 ; B ; C . Các giá trị của tham số m để B C = 4 là:
A. m = ± 2
B. m = ± 4
C. m = 4
D. m = 2
Những câu hỏi liên quan
22 tháng 8 2021 lúc 20:34
Câu 3 Để đồ thị hàm số \(y=-x^4-\left(m-3\right)x^2+m+1\) có điểm cực đạt mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là
Câu 4 Cho hàm số \(y=x^4-2mx^2+m\) .Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị
tìm m để đồ thị hàm số \(\left(C_m\right):y=x^3-3mx^2+3\left(m^2-1\right)x-m^3+m\) có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số O bằng √2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến O ( O là gốc tọa độ )
Lời giải:
$y'=3x^2-6mx+3(m^2-1)=0$
$\Leftrightarrow x^2-2mx+m^2-1=0$
$\Leftrightarrow x=m+1$ hoặc $x=m-1$
Với $x=m+1$ thì $y=-2m-2$. Ta có điểm cực trị $(m+1, -2m-2)$
Với $x=m-1$ thì $y=2-2m$. Ta có điểm cực trị $m-1, 2-2m$
$f''(m+1)=6>0$ nên $A(m+1, -2m-2)$ là điểm cực tiểu
$f''(m-1)=-6< 0$ nên $B(m-1,2-2m)$ là điểm cực đại
$BO=\sqrt{2}AO$
$\Leftrightarrow BO^2=2AO^2$
$\Leftrightarrow (m-1)^2+(2-2m)^2=2(m+1)^2+2(-2m-2)^2$
$\Leftrightarrow m=-3\pm 2\sqrt{2}$
Đúng 2
Bình luận (0)
Cho hai hàm đa thức y f(x), y g(x) có đồ thị là hai đường cong ở hình vẽ. Biết rằng đồ thị hàm số y f(x) có đúng một điểm cực trị là A, đồ thị hàm số y g(x) có đúng một điểm cực trị là B và
A
B
7
4
.
Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (-5;5) để hàm số
y
f
(
x
)...
Đọc tiếp
Cho hai hàm đa thức y = f(x), y = g(x) có đồ thị là hai đường cong ở hình vẽ. Biết rằng đồ thị hàm số y = f(x) có đúng một điểm cực trị là A, đồ thị hàm số y = g(x) có đúng một điểm cực trị là B và A B = 7 4 . Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (-5;5) để hàm số y = f ( x ) - g ( x ) + m có đúng 5 điểm cực trị?
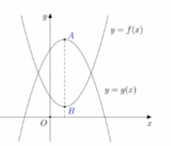
A. 1
B. 3
C. 4
D. 6
Cho hàm số y = x^4 + 2(m + 1)x^2 + 1
a) Khảo sát và vẽ đồ thị khi m = 1
b) Tìm m để đồ thị hàm số có 3 điểm cực trị. Tìm phương trình đường cong đi qua các điểm cực trị đó
b.
y = x^4 + 2(m + 1)x^2 + 1
y' = 4x^3 + 4(m + 1)x
y'= 0=> x=0 và x^2 + (m + 1)= 0 (*)
để đồ thị hàm số có 3 điểm cực trị thì (*) có 2 nghiệm phân biệt
=> m+1<0
<=> m< -1
ta có:
y= [4x^3 + 4(m + 1)x]*x/4+ (m+1)x^2+ 1
y= y'*x/4+ (m+1)x^2+ 1
đường cong đi qua các điểm cực trị thỏa mãn y'= 0
=> pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
Vậy để đồ thị hàm số có 3 điểm cực trị thì m< -1
và pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
Đúng 0
Bình luận (0)
b.
y = x^4 + 2(m + 1)x^2 + 1
y' = 4x^3 + 4(m + 1)x
y'= 0=> x=0 và x^2 + (m + 1)= 0 (*)
để đồ thị hàm số có 3 điểm cực trị thì (*) có 2 nghiệm phân biệt
=> m+1<0
<=> m< -1
ta có:
y= [4x^3 + 4(m + 1)x]*x/4+ (m+1)x^2+ 1
y= y'*x/4+ (m+1)x^2+ 1
đường cong đi qua các điểm cực trị thỏa mãn y'= 0
=> pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
Vậy để đồ thị hàm số có 3 điểm cực trị thì m< -1
và pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
Đúng 0
Bình luận (0)
Cho hàm số
y
f
(
x
)
có đồ thị như hình vẽ. Biết tất cả các điểm cực trị của hàm số
y
f
(
x
)
là – 2, 0, 2, a , 6 với 4 a 6. Số điểm cực trị của hàm số
y
f
(
x
6
−
3
x
2
)
là A. 8 B. 11 C. 9 D. 7
Đọc tiếp
Cho hàm số y = f ( x ) có đồ thị như hình vẽ.
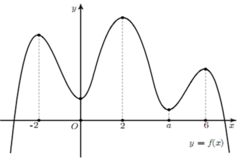
Biết tất cả các điểm cực trị của hàm số y = f ( x ) là – 2, 0, 2, a , 6 với 4 < a < 6. Số điểm cực trị của hàm số y = f ( x 6 − 3 x 2 ) là
A. 8
B. 11
C. 9
D. 7
tìm m để đồ thị hàm số \(\left(C_m\right):y=x^3-3mx^2+3\left(m^2-1\right)x-m^3+m\) có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số O bằng \(\sqrt{2}\) lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến O ( O là gốc tọa độ )
Cho hai hàm số
f
(
x
)
x
4
-
m
-
1
x
2
+
2
và
g
(
x
)
2
x
4
-
4
x...
Đọc tiếp
Cho hai hàm số f ( x ) = x 4 - m - 1 x 2 + 2 và g ( x ) = 2 x 4 - 4 x 2 + 3 m . Giả sử đồ thị hàm số f(x) có ba điểm cực trị là A, B, C và đồ thị hàm số g(x) có ba điểm cực trị là M, N, P. Có bao nhiêu giá trị của tham số m để hai tam giác ABC và MNP đồng dạng với nhau?
A. 1.
B. 0.
C. 2.
D. 3.
Có bao nhiêu số nguyên m thuộc [-20;20] để đồ thị hàm số y=mx^4+(m^2-9)x^2+1 có ba điểm cực trị?
A. 20. B. 19. C. 18. D. 17.
Có bao nhiêu số nguyên m thuộc [-20;20] để đồ thị hàm số
y=mx4+(m2-9)x2+1 có ba điểm cực trị?
A. 20. B. 19. C. 18. D. 17.
y' = 4mx3 + 2(m2-9)x
hàm số có 3 điểm cực trị => m ≠ 0 và m.(m2-9)<0
=> x < -3 và 0 < x < 3
=> x ∈ {-20;-19;-18;...;-4;1;2} => 19 giá trị
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hàm số bậc ba
y
ax
3
+
bx
2
+
cx
+
d
có đồ thị nhận hai điểm A(0;3) và B(2;-1) làm hai điểm cực trị. Khi đó số điểm cực trị của hàm số
y
|
ax...
Đọc tiếp
Cho hàm số bậc ba y = ax 3 + bx 2 + cx + d có đồ thị nhận hai điểm A(0;3) và B(2;-1) làm hai điểm cực trị. Khi đó số điểm cực trị của hàm số y = | ax 2 | x | + bx 2 + c | x | + d | là
A. 5
B. 7
C. 9
D. 11
Cho hàm số bậc ba yf(x) có đồ thị như hình vẽ bên. Tất cả giá trị thực của tham số m để hàm số
y
f
(
x
-
1
)
-
m
-
1
có 3 điểm cực trị? A. -1m5 B.
-
1
≤
m
≤
5
C.
m...
Đọc tiếp
Cho hàm số bậc ba y=f(x) có đồ thị như hình vẽ bên. Tất cả giá trị thực của tham số m để hàm số y = f ( x - 1 ) - m - 1 có 3 điểm cực trị?
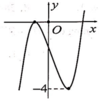
A. -1<m<5
B. - 1 ≤ m ≤ 5
C. m ≥ - 1 hoặc m ≤ - 5
D. m>-1 hoặc m<-5
