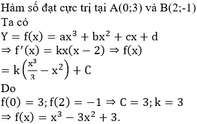Các câu hỏi tương tự
Cho hàm số
y
a
x
3
+
b
x
2
+
c
x
+
d
có đồ thị nhận hai điểm A(0;3) và B(2;-1) làm hai điểm cực trị. Số điểm cực trị của đồ thị hàm số
y
a
x
2
x
+
b...
Đọc tiếp
Cho hàm số y = a x 3 + b x 2 + c x + d có đồ thị nhận hai điểm A(0;3) và B(2;-1) làm hai điểm cực trị. Số điểm cực trị của đồ thị hàm số y = a x 2 x + b x 2 + c x + d là:
A. 7
B. 5
C. 9
D. 11
Cho hàm số
y
f
x
a
x
3
+
b
x
2
+
c
x
+
d
có đồ thị (C). Biết đồ thị hàm số (C) có hai điểm cực trị A(2;-27) ; B(-4;81). Tính S-a+b-c+d A. S 24 B. S 27 C. S 31 D. S 32
Đọc tiếp
Cho hàm số y = f x = a x 3 + b x 2 + c x + d có đồ thị (C). Biết đồ thị hàm số (C) có hai điểm cực trị A(2;-27) ; B(-4;81). Tính S=-a+b-c+d
A. S = 24
B. S = 27
C. S = 31
D. S = 32
Biết
M
−
2
;
5
,
N
0
;
13
là các điểm cực trị của đồ thị hàm số
y
a
x
+
b
+
c
x
+
1
.
Tính giá trị của hàm số tại x 2 A.
-...
Đọc tiếp
Biết M − 2 ; 5 , N 0 ; 13 là các điểm cực trị của đồ thị hàm số y = a x + b + c x + 1 . Tính giá trị của hàm số tại x = 2
A. - 13 3
B. 16 9
C. 16 3
D. 47 3
Cho hàm số
y
f
x
a
x
3
+
b
x
2
+
c
x
+
d
có hai cực trị
x
1
,
x
2
thỏa mãn
-
2
x
1
0
x
2...
Đọc tiếp
Cho hàm số y = f x = a x 3 + b x 2 + c x + d có hai cực trị x 1 , x 2 thỏa mãn - 2 < x 1 < 0 < x 2 < 2 và có đồ thị như hình vẽ.
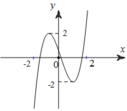
Số điểm cực tiểu của hàm số y = f(x) là
A. 3.
B. 5.
C. 7.
D. 4.
Đồ thị hàm số y = f(x) = x 3 + a x 2 + b x + c có hai điểm cực đại là A ( -2;16 ) và B ( 2;-16 ). Tính a + b + c
A. -12
B. 0
C. -6
D. -3
Biết đồ thị hàm số
y
a
x
3
+
b
x
2
+
c
x
+
d
có 2 điểm cực trị là
−
1
;
18
và
3
;
−
16
.
. Tính tổng
a
+
b...
Đọc tiếp
Biết đồ thị hàm số y = a x 3 + b x 2 + c x + d có 2 điểm cực trị là − 1 ; 18 và 3 ; − 16 . . Tính tổng a + b + c + d .
A. 1.
B. 3.
C. 2.
D. 0.
Đồ thị hàm số
y
a
x
3
+
b
x
2
+
c
x
+
d
có hai điểm cực trị là
A
(
0
;
0
)
và
B
(
1
;
1
)
. Khi đó
a
2
+
b
2
+
c
2
+
d
2
là: A. 13 B. 14 C. 11 D. 9
Đọc tiếp
Đồ thị hàm số y = a x 3 + b x 2 + c x + d có hai điểm cực trị là A ( 0 ; 0 ) và B ( 1 ; 1 ) . Khi đó a 2 + b 2 + c 2 + d 2 là:
A. 13
B. 14
C. 11
D. 9
Biết đồ thị hàm số
y
x
2
-
3
x
+
m
x
+
3
(m là tham số) có ba điểm cực trị. Parabol
y
a
x
2
+
b
x
+
c
đi qua ba điểm cực trị đó. Tính
a
+
2
b
+
4
c
A.
a
+...
Đọc tiếp
Biết đồ thị hàm số y = x 2 - 3 x + m x + 3 (m là tham số) có ba điểm cực trị. Parabol y = a x 2 + b x + c đi qua ba điểm cực trị đó. Tính a + 2 b + 4 c
A. a + 2 b + 4 c = 3
B. a + 2 b + 4 c = 0
C. a + 2 b + 4 c = - 4
D. a + 2 b + 4 c = 1
Cho hàm số
y
e
a
x
2
+
b
x
+
c
đạt cực trị tại x1 và đồ thị hàm số cắt trục tung tại điểm có tung độ bằng e. Tính giá trị của hàm số tại x2? A.
y
2
e
2
B.
y
2...
Đọc tiếp
Cho hàm số y = e a x 2 + b x + c đạt cực trị tại x=1 và đồ thị hàm số cắt trục tung tại điểm có tung độ bằng e. Tính giá trị của hàm số tại x=2?
A. y 2 = e 2
B. y 2 = 1 e 2
C. y 2 = 1
D.. y 2 = e