Cho tứ diện ABCD có A(0;1;-1), B(1;1;2), C(1;-1;0), D(0;0;1). Tính độ dài đường cao AH của hình chóp ABCD.
A. 3 2
B. 2 2
C. 2 2
D. 3 2 2
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau, biết rằng AB = a; AC =a 2 ; AD = a 3 ,(a>0) Thể tích V của khối tứ diện ABCD là:
A. V = a 3 6 3
B. V = a 3 6 6
C. V = a 3 6 2
D. V = a 3 6 9
Đáp án B
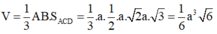
Phương án nhiễu.
A. Sai vì 2 cách: một là thấy số 1 3 cứ chọn, hai là trong công thức thể tích thiếu 1 3 diện tích đáy.
C. Sai vì thiếu 1 3 trong công thức thể tích.
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau, biết rằng A B = a , A C = a 2 , A D = a 3 , a > 0 . Thể tích V của khối tứ diện ABCD là:
A. V = 1 3 a 3 6
B. V = 1 6 a 3 6
C. V = 1 2 a 3 6
D. V = 1 9 a 3 6
Cho tứ diện ABCD. Hỏi có bao nhiêu vectơ khác vectơ 0 → mà mỗi vectơ có điểm đầu, điểm cuối là hai đỉnh của tứ diện ABCD
A. 12
B. 4
C. 10
D. 8
Đáp án A.
Với mỗi cách chọn ra 2 đỉnh bất kỳ của tứ diện ta được 2 vecto đối nhau.
Do đó có 2 C 4 2 = 12 vecto.
Cho tứ diện ABCD, hỏi có bao nhiêu véctơ khác véctơ 0 → mà mỗi véctơ có điểm đầu, điểm cuối là hai đỉnh của tứ diện ABCD
A. 4.
B. 12.
C. 10.
D. 8.
Đáp án là B
Mỗi cạnh của tứ diện tạo thành 2 vecto thỏa mãn đề bài, suy ra có 6.2 = 12 vecto.
Cho tứ diện ABCD, hỏi có bao nhiêu véctơ khác véctơ 0 ⇀ mà mỗi véctơ có điểm đầu, điểm cuối là hai đỉnh của tứ diện ABCD
A. 4.
B. 12.
C. 10.
D. 8.
Đáp án B.
Mỗi cạnh của tứ diện tạo thành 2 vecto thỏa mãn đề bài, suy ra có 6.2=12 vecto
Cho tứ diện ABCD. Hỏi có bao nhiêu vectơ khác vectơ 0 → mà mỗi vectơ có điểm đầu, điểm cuối là hai đỉnh của tứ diện ABCD ?
A. 12
B. 4
C. 10
D. 8
Chọn A
Số vectơ khác vectơ 0 → mà mỗi vectơ có điểm đầu, điểm cuối là hai đỉnh của tứ diện ABCD là số các chỉnh hợp chập 2 của phần tử => số vectơ là A 4 2 = 12
Cho tứ diện ABCD. Hỏi có bao nhiêu vectơ khác vectơ 0 ⇀ mà mỗi vectơ có điểm đầu, điểm cuối là hai đỉnh của tứ diện ABCD
A. 12.
B. 4.
C. 10.
D. 8
Đáp án A.
Với mỗi cách chọn ra 2 đỉnh bất kỳ của tứ diện ta được 2 vecto đối nhau.
Do đó có 2 C 4 2 = 12 vecto.
Cho tứ diện đều ABCD có cạnh bằng a,điểm M trên cạnh AB sao cho AM=m(0<m<a). Khi đó diện tích thiết diện của hình tứ diện cắt bởi mp qua M và song song với mp(ACD) là:
A. 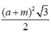
B. ![]()
C. ![]()
D. ![]()
Đáp án B
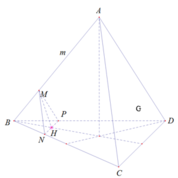
Trong (ABC) kẻ MN // AC ( N ∈ BC)
Trong (ABD) kẻ MP // AD ( P ∈ BD)
⇒ (MNP) là mặt phẳng cần tìm
Xét tam giác MNP có MN = MP =NP (= a - m )
⇒ tam giác MNP đều
Mà NP // CD và BG là trung tuyến tam giác BCD
⇒ BG cắt NP tại H là trung điểm NP
⇒ MH là đường cao tam giác MNP
Ta có: PH = a - m 2 và MP = a – m. Áp dụng định lý pitago, ta có: MH = 3 2 a - m
Và NP = a – m
SMNP = MH . NP 2 = 3 4 a - m 2
Trong không gian Oxyz, cho hai mặt cầu S 1 : x 2 + y 2 + z 2 - 2 x + 4 y - 2 z + 2 = 0 và S 2 : x 2 + y 2 + z 2 - 2 x + 4 y - 2 z - 4 = 0 . Xét tứ diện ABCD có hai đỉnh A,B nằm trên (S1); hai đỉnh C,D nằm trên (S2 ). Thể tích khối tứ diện ABCD có giá trị lớn nhất bằng
A. 3 2
B. 2 3
C. 6 3
D. 6 2
Trong không gian Oxyz, cho hai mặt cầu ( S 1 ) : x 2 + y 2 + z 2 - 2 x + 4 y - 2 z + 2 = 0 và ( S 2 ) : x 2 + y 2 + z 2 - 2 x + 4 y - 2 z - 4 = 0 . Xét tứ diện ABCD có hai đỉnh A, B nằm trên S1; hai đỉnh C,D nằm trên S2. Thể tích khối tứ diện ABCD có giá trị lớn nhất bằng
A. 3 2
B. 2 3
C. 6 3
D. 6 2