Cho x,y là hai số không âm thỏa mãn x+y=2. Giá trị nhỏ nhất của biểu thức P = 1 3 x 3 + x 2 + y 2 − x + 1 là:
A. min P = 7 3
B. min P = 5
C. min P = 17 3
D. min P = 115 3
Cho x, y là hai số không âm thỏa mãn x + y = 2. Giá trị nhỏ nhất của biểu thức
P
=
1
3
x
3
+
x
2
+
y
2
−
x
+
1
A. min P = 5
B. min P = 115 3
C. min P = 7 3
D. min P = 17 3
Chọn C.
Phương pháp:
Đưa biểu thức P về hàm số 1 ẩn x.
Khảo sát, tìm GTNN của hàm số đó.
Cách giải:
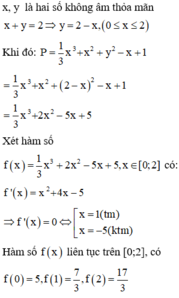
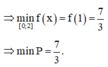
Cho x, y là hai số không âm thỏa mãn x+y=2 Giá trị nhỏ nhất của biểu thức
P = 1 3 x 3 + x 2 + y 2 - x + 1
A. 5
B. 115 3
C. 7 3
D. 17 3
Cho x, y là hai số không âm thỏa mãn x + y = 2. Giá trị nhỏ nhất của biểu thức P = 1 3 x 3 + x 2 + y 2 - x + 1
A. m i n P = 5
B. m i n P = 7 3
C. m i n P = 17 3
D. m i n P = 115 3
Cho x và y là hai số thực không âm thỏa mãn x + y = 4 . Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức P = \(x^4+y^4-4xy+3\)
\(P=\left(x^2+y^2\right)^2-2x^2y^2-4xy+3=\left[\left(x+y\right)^2-2xy\right]^2-2x^2y^2-4xy+3\)
\(=\left(16-2xy\right)^2-2x^2y^2-4xy+3=2x^2y^2-68xy+259\)
\(4=x+y\ge2\sqrt[]{xy}\Rightarrow0\le xy\le4\)
Đặt \(xy=a\Rightarrow0\le a\le4\)
\(P=2a^2-68a+259=259-2a\left(34-a\right)\le259\)
\(P_{max}=259\) khi \(a=0\) hay \(\left(x;y\right)=\left(4;0\right);\left(0;4\right)\)
\(P=\left(2a^2-68a+240\right)+19=2\left(4-a\right)\left(30-a\right)+19\ge19\)
\(P_{min}=19\) khi \(a=4\) hay \(x=y=2\)
Cho x, y là hai số không âm thỏa mãn x + y =2. Giá trị nhỏ nhất của biểu thức P = 1 3 x 3 + x 2 + y 2 - x + 1 là
A. 17 3
B. 5
C. 115 3
D. 7 3
Cho x,y là hai số không âm thỏa mãn x + y = 2. Tìm giá trị nhỏ nhất của biểu thức P = 1 3 x 3 + x 2 + y 2 - x + 1
A. 5
B. 7 3
C. 17 3
D. 115 3
Ta có x + y = 2 ⇒ y = 2 - x ≥ 0 ⇒ 0 ≤ x ≤ 2 . Thay y = 2 - x và biểu thức P ta được
P = 1 3 x 3 + x 2 + 2 - x 2 - x + 1 = 1 3 x 3 + 2 x 2 - 5 x + 5 = f x
với x ∈ 0 ; 2
Đạo hàm f ' x = x 2 + 4 x - 5 = 0 ⇔ x = 1 x = - 5
Do x ∈ 0 ; 2 nên loại x = -5
f 1 = 7 3 ; f 0 = 5 ; f 2 = 17 3
Vậy m i n x ∈ 0 ; 2 P = m i n x ∈ 0 ; 2 f x = 7 3 khi và chỉ khi x = 1
Đáp án B
cho x,y là hai số thực không âm thỏa mãn (x+1)(y+1)=9. tính giá trị nhỏ nhất,lớn nhất của biểu thức k= x^2+y^2
\(\left(x+1\right)\left(y+1\right)=9\)
\(\Rightarrow xy+x+y+1=9\)
\(\Rightarrow xy+x+y=8\)
\(\Rightarrow x+y=8-xy\left(1\right)\)
\(K=x^2+y^2\)
\(\Rightarrow K=\left(x+y\right)^2-2xy=\left(8-xy\right)^2-2xy\)
\(\Rightarrow K=64-16xy+\left(xy\right)^2-2xy\)
\(\Rightarrow K=\left(xy\right)^2-18xy+64\)
\(\Rightarrow K=\left(xy\right)^2-18xy+81-17\)
\(\Rightarrow K=\left(xy-9\right)^2-17\ge-17\left(\left(xy-9\right)^2\ge0,\forall x;y\right)\)
\(\Rightarrow GTNN\left(K\right)=-17\)
Cho các số x,y là các số thực không đổi âm thỏa mãn x+y = 1. Tìm giá trị nhỏ nhất của biểu thức \(A=x^3+y^3\)
\(x+y=1\ge2\sqrt{xy}\Rightarrow xy\le\frac{1}{4}\)
=> \(A=x^3+y^3=\left(x+y\right)^3-3xy.\left(x+y\right)\ge1^2-3\cdot\frac{1}{4}\cdot1=\frac{1}{4}\)
Dấu "=" xảy ra <=> x=y=\(\frac{1}{2}\)
vậy ...
\(\left(x-y\right)^2\ge0\Leftrightarrow x^2+y^2\ge2xy\Leftrightarrow\left(x+y\right)^2\ge4xy\Leftrightarrow xy\le\frac{\left(x+y\right)^2}{4}=\frac{1}{4}\)
\(A=x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)=1-3xy\ge1-3.\frac{1}{4}=\frac{1}{4}\)
Dấu \(=\)khi \(x=y=\frac{1}{2}\).
Cho x, y, z là các số thực không âm thỏa mãn \(x^2+y^2+z^2=4\). Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức P=x+y+z
Ta có :
\(\left(1^2+1^2+1^2\right)\left(x^2+y^2+z^2\right)\ge\left(1.x+1.y+1.z\right)^2\) (Bunhia)
\(\Leftrightarrow3\left(x^2+y^2+z^2\right)\ge\left(x+y+z\right)^2\)
\(\Leftrightarrow\left(x+y+z\right)^2\le3.4=12\)
\(\Rightarrow-2\sqrt{3}\le x+y+z\le2\sqrt{3}\)
Bạn trên làm sai r. X+y+z ko âm cơ mà sao lại có gtnn là -2√3??