Cho H là hình phẳng giới hạn bởi parabol ( P ) :   y = x 2 , tiếp tuyến với (P) tại M(2;4) và trục hoành. Tính diện tích của hình phẳng (H)?

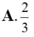
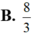
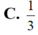
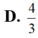
Cho parabol ( P ) :   y = x 2 + 2  và hai tiếp tuyến của (P) tại các điểm M(-1;3) và N(2;6). Diện tích hình phẳng  giới hạn bởi (P) và hai tiếp tuyến đó bằng

A.  9 4

B.  13 4

C.  7 4

D.  21 4

Diện tích S của hình phẳng giới hạn bởi parabol ( P ) : y = x 2 - 1 ,  tiếp tuyến của (P) tại M(0;1) và trục Oy là:

A. S = 1.

B .   S   =   1 4 .  

C .   S   =   1 3 .  

D .   S   =   7 3 .    

Diện tích S của hình phẳng giới hạn bởi đường (P) y   =   2 x 2  parabol tiếp tuyến của (P) tại M (1;2) và trục Oy là

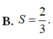
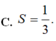
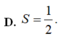
Cho parabol P : y = x 2 + 2 và hai tiếp tuyến của (P) tại các điểm M - 1 ; 3 và N 2 ; 6 .  Diện tích hình phẳng giới hạn bởi (P) và hai tiếp tuyến đó bằng

A.  9 4

B.  13 4

C.  7 4

D.  21 4

Cho Parabol P : y = 2 x 2 . Gọi d là tiếp tuyến với (P) tại điểm có hoành độ bằng 2. Tính diện tích hình phẳng giới hạn bởi đồ thị (P), đường thẳng d và đường thẳng x=1.

A. 2 3

B.  1 2

C.  1 3

D.  3 2

Diện tích S của hình phẳng giới hạn bởi đường P : y = 2 x 2 ,  parabol tiếp tuyến của (P) tại M (1;2) và trục Oy là

A.  S = 1.

B.  S = 2 3 .

C.  S = 1 3 .

D.  S = 1 2 .

Cho hình phẳng (H) giới hạn bởi parabol P : y = x 2 , trục hoành và tiếp tuyến của (P) tại điểm M(2;4). Tính thể tích V của khối tròn xoay tạo thành khi quay hình (H) xung quanh trục hoành.

A.  77π/15

B.  64π/15

C.  176π/15

D.  16π/15