Cho đồ thị của hàm số y = x 3 - 3 x 2 + 1 như hình vẽ.
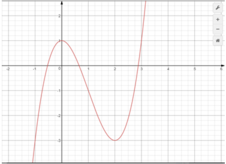
Khi đó, phương trình x 3 - 3 x 2 + 1 = m (m là tham số ) có 3 nghiệm phân biệt khi và chỉ khi:
A. - 3 < m < 1
B. m > 1
C. m < - 3
D. - 3 ≤ m ≤ 1
Cho đồ thị của hàm số \(y = {2^x}\) và \(y = 4\) như Hình 6.7. Tìm khoảng giá trị của x mà đồ thị hàm số \(y = {2^x}\) nằm phía trên đường thẳng y = 4 và từ đó suy ra tập nghiệm của bất phương trình \({2^x} > 4.\)

Khoảng giá trị của x mà đồ thị hàm số \(y = {2^x}\) nằm phía trên đường thẳng y = 4 là \(\left( {2; + \infty } \right)\)
Vậy tập nghiệm của bất phương trình \({2^x} > 4\) là \(\left( {2; + \infty } \right)\)
Cho hàm số y = f(x) đồ thị như hình vẽ
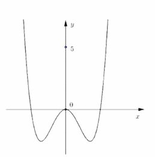
Số nghiệm thực của phương trình f(x) = 3 là
A. 0.
B. 3.
C. 1.
D. 2.
Cho hàm số y=f(x) có đồ thị như hình vẽ. Số nghiệm của phương trình 2f(x)=3 là
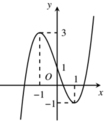
A. 3
B. 2
C. 1
D. 0
Cho đồ thị của hàm số \(y = {\log _2}x\) và y = 2 như Hình 6.8. Tìm khoảng giá trị của x mà đồ thị hàm số \(y = {\log _2}x\) nằm phía trên đường thẳng y = 2 và từ đó suy ra tập nghiệm của bất phương trình \({\log _2}x > 2.\)

Khoảng giá trị của x mà đồ thị hàm số \(y=log_2x\) nằm phía trên đường thẳng y = 2 là \(\left(4;+\infty\right)\)
\(\Rightarrow\) Tập nghiệm của bất phương trình \(log_2x>2\) là \(\left(4;+\infty\right)\)
Cho hàm số y=f(x) có đồ thị như hình vẽ. Số nghiệm của phương trình 2 f ( x ) - 3 = 0 là
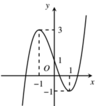
A. 3
B. 2
C. 1
D. 0
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
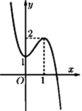
Số nghiệm của phương trình 2 f x − 1 − 3 = 0 là
A. 1.
B. 4.
C. 3.
D. 2.
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
Số nghiệm của phương trình 2 f x - 1 - 3 = 0 là:
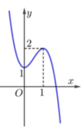
A. 1
B. 4
C. 3
D. 2
Đáp án B
2 f x - 1 - 3 = 0 ⇔ f x - 1 = 3 2
Đồ thị hàm số y = f x - 1 có được bằng cách tình tiến đồ thị hàm số y = f(x) sang phải một đơn vị, sau đó lấy đối xứng đồ thị vừa tịnh tiến được qua trục Ox
Ta thấy f x - 1 = 3 2 là sự tương giao giữa đồ thị hàm số y = f x - 1 và đường thẳng y = 3 2 . Dựa vào đồ thị hàm số ta thấy f x - 1 = 3 2 có 4 nghiệm
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Số nghiệm của phương trình
2
f
x
-
1
-
3
=
0
là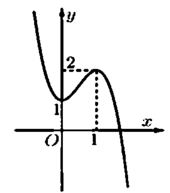
A. 1
B. 4
C. 3
D. 2
Đáp án B
Cách 1:
Dựa vào đồ thị suy ra hàm số có dạng bậc 3
Ta có y ' = k x x - 1 ⇒ y = k x 3 2 - x 2 2 + C
Đồ thị qua 2 điểm (0;1),(1;2)
⇒ C = 1 k = - 6 ⇒ y = - 2 x 3 + 3 x 2 + 1 . Từ đó vẽ đồ thị hàm số y = f x - 1
Cách 2:
Từ đồ thị hàm số y = f(x) tịnh tiến sang phải 1 đơn vị ta được đồ thị hàm số y = f(x - 1) từ đó suy ra đồ thị hàm số
y
=
f
x
-
1
như hình bên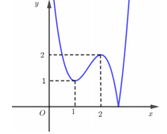
Suy ra phương trình f x - 1 = 3 2 có 4 nghiệm phân biệt
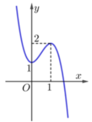
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
Số nghiệm của phương trình 2 f x − 1 − 3 = 0 là:
A. 1
B. 4
C. 3
D. 2
Đáp án B
2 f ( x − 1 ) − 3 = 0 ⇔ f ( x − 1 ) = 3 2
Đồ thị hàm số y = f ( x − 1 ) có được bằng cách tình tiến đồ thị hàm số y = f(x) sang phải một đơn vị, sau đó lấy đối xứng đồ thị vừa tịnh tiến được qua trục Ox
Ta thấy f ( x − 1 ) = 3 2 là sự tương giao giữa đồ thị hàm số y = f ( x − 1 ) và đường thẳng y = 3 2 . Dựa vào đồ thị hàm số ta thấy f ( x − 1 ) = 3 2 có 4 nghiệm
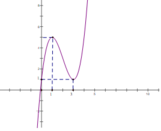
Cho hàm số bậc ba y=f(x) có đồ thị như hình vẽ bên. Số nghiệm của phương trình f(x)=3
A. 0
B. 2
C. 1
D. 3