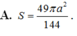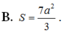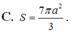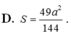Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh a. Cạnh bên AA'=a 2 . Thể tích khối lăng trụ ABC.A'B'C' là:

A.  V = a 3 6 4

B.  V = a 3 6 2

C.  V = a 3 6 12

D.  V = a 6 4

a) Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, AB=a. Biết diện tích tứ giác ABB'A' bằng \(2a^2\), thể tích khối lăng trụ ABC.A'B'C' bằng?

b) Cho hình lăng trụ đúng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, AB=a. Biết góc giữa (AB'C') và (A'B'C') bằng 60°, thể tích khối lăng trụ ABC.A'B'C' bằng?

Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông tại A, A B C ⏜ = 30 0 . Gọi M là trung điểm của AB, tam giác MA'C đều cạnh 2a 3  và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối lăng trụ là ABC.A'B'C'

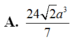
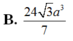
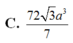
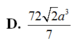
Cho hình lăng trụ tam giác đều ABC.A'B'C' có AA' = a 3 , AB = a. Gọi M là trung điểm BC. Tính thể tích V của hình chóp AMB’C’.

A. V =  a 3 3 4

B. V = a 3 3

C. V = a 3 4

D. V = a 3 3 2

Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh  a, biết A A = A B = A C = a  . Tính thể tích khối lăng trụ  A B C . A ' B ' C '

A.  3 a 3 4  

B.  a 3 2 4  

C.  a 3 3 4  

D.  a 3 4  

Cho hình lăng trụ tam giác đều ABC.A'B'C' có AB=2a, AA'=a 3 . Tính thể tích khối lăng trụ ABC.A'B'C'.

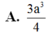
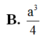
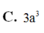
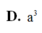
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông tại A ,    A B C ^ = 30 ° . Gọi M là trung điểm của AB, tam giác MA'C đều cạnh 2 a 3  và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối lăng trụ là ABC.A'B'C'

A.  24 2 a 3 7

B.  24 3 a 3 7

C.  72 3 a 3 7

D.  72 2 a 3 7

Cho hình lăng trụ tam giác A B C . A ' B ' C '  có đáy là tam giác đều cạnh a Cạnh bên tạo với đáy một góc 60 0 .  Gọi M là trung điểm của B ' C ' và I là trung điểm của đoạn A ' M . Biết hình chiếu vuông góc của I trên mặt phẳng đáy A B C  là trọng tâm cả tam giác A B C .  Tính thể tích của khối lăng trụ A B C . A ' B ' C '  theo

A.  a 3 3 4 .

B.  a 3 3 48 .

C.  a 3 3 16 .

D.  a 3 3 12 .

Cho hình lăng trụ tam giác đều A B C . A ' B ' C '  có tất cả các cạnh bằng a. Diện tích mặt cầu ngoại tiếp hình lăng trụ  A B C . A ' B ' C ' là: