Một con lắc đơn dao động điều hoà với phương trình li độ góc α = 0 , 1 cos 2 πt rad . Lấy g = 10 m / s 2 và π 2 = 10 . Khi qua vị trí cân bằng vật có tốc độ là
A. 20 π cm / s
B. 5 π cm / s
C. 50 cm / s
D. 0 , 2 π cm / s
Những câu hỏi liên quan
Một con lắc đơn dài 1,5 m dao động điều hòa với phương trình li độ góc
α
0
,
1
c
o
s
(
2
t
+
π
)
(rad) (t tính bằng s). Tại thời điểm t 0,5
π
s thì li độ dài của con lắc là A. 0,15 cm B. 0,1 cm C. 10 cm D. 0,15 m
Đọc tiếp
Một con lắc đơn dài 1,5 m dao động điều hòa với phương trình li độ góc α = 0 , 1 c o s ( 2 t + π ) (rad) (t tính bằng s). Tại thời điểm t = 0,5 π s thì li độ dài của con lắc là
A. 0,15 cm
B. 0,1 cm
C. 10 cm
D. 0,15 m
Chọn đáp án D
t = 0 , 5 π ( s )
⇒ α 1 = 0 , 1. cos 2.0 , 5 π + π = 0 , 1 ( r a d )
⇒ s 1 = l . α = 1 , 5.0 , 1 = 0 , 15 ( m )
Đúng 0
Bình luận (0)
Một con lắc đơn dài 1,5 m dao động điều hòa với phương trình li độ góc α 0,1cos(2t +
π
) (rad) (t tính bằng s). Tại thời điểm t 0,5
π
s thì li độ dài của con lắc là A. 0,15 cm B. 0,1 cm C. 10 cm D. 0,15 m
Đọc tiếp
Một con lắc đơn dài 1,5 m dao động điều hòa với phương trình li độ góc α = 0,1cos(2t + π ) (rad) (t tính bằng s). Tại thời điểm t = 0,5 π s thì li độ dài của con lắc là
A. 0,15 cm
B. 0,1 cm
C. 10 cm
D. 0,15 m
Một con lắc đơn dao động điều hòa với chu kì T 2 s. Lấy g 10 ≈
π
2
m/
s
2
. Tại thời điểm ban đầu vật có li độ góc α 0,05 rad và vận tốc v – 15,7 cm/s. Phương trình dao động của con lắc là: A.
s
5
2
cos
πt
+
π
4...
Đọc tiếp
Một con lắc đơn dao động điều hòa với chu kì T = 2 s. Lấy g = 10 ≈ π 2 m/ s 2 . Tại thời điểm ban đầu vật có li độ góc α = 0,05 rad và vận tốc v = – 15,7 cm/s. Phương trình dao động của con lắc là:
A. s = 5 2 cos πt + π 4 cm
B. s = 5 2 cos πt − π 4 cm
C. s = 5 2 cos 2 πt + π 4 cm
D. s = 5 2 cos 2 πt − π 4 cm
Con lắc đơn chiều dài 40cm đang đứng yên ở vị trí cân bằng. Lúc t 0 truyền cho con lắc vận tốc v0 20cm/s nằm ngang theo chiều dương thì nó dao động điều hoà với chu kì T 2π/5(s). Phương trình dao động của con lắc dạng li độ góc là: A. α 0,1sin(t/5)(rad). B. α 0,1sin(t/5 + π)(rad). C. α 0,1cos(5t- π/2) (rad). D. α 0,1sin(5t + π) (rad).
Đọc tiếp
Con lắc đơn chiều dài 40cm đang đứng yên ở vị trí cân bằng. Lúc t = 0 truyền cho con lắc vận tốc v0 = 20cm/s nằm ngang theo chiều dương thì nó dao động điều hoà với chu kì T = 2π/5(s). Phương trình dao động của con lắc dạng li độ góc là:
A. α = 0,1sin(t/5)(rad).
B. α = 0,1sin(t/5 + π)(rad).
C. α = 0,1cos(5t- π/2) (rad).
D. α = 0,1sin(5t + π) (rad).
Chọn C
+ ω = 2π/T = 5 (rad/s)
+ vmax = ωA => A = vmax : ω = 0,2 : 5 = 0,04m => αo = A/l = 0,04/0,4 = 0,1 rad.
+ t = 0: α = 0,1cosφ = 0 và v = -0,5sinφ > 0 => φ = -π/2 (rad)
Vậy: α = 0,1cos(5t - π/2) (rad).
Đúng 0
Bình luận (0)
Một con lắc đơn dao động điều hoà với phương trình s 6cos(0,5πt-π/2)(cm). Khoảng thời gian ngắn nhất để con lắc đi từ vị trí có li độ s 3cm đến li độ cực đại S0 6cm là: A. 1/3s. B. 4s. C. 2/3s. D. 1s.
Đọc tiếp
Một con lắc đơn dao động điều hoà với phương trình s = 6cos(0,5πt-π/2)(cm). Khoảng thời gian ngắn nhất để con lắc đi từ vị trí có li độ s = 3cm đến li độ cực đại S0 = 6cm là:
A. 1/3s.
B. 4s.
C. 2/3s.
D. 1s.
Chọn C
+ T = 2 π w = 4 s
+ Khoảng thời gian ngắn nhất để con lắc đi từ vị trí có li độ s = 3cm đến li độ cực đại S0 = 6cm: t = T 6 = 4 6 = 2 3 s .
Đúng 0
Bình luận (0)
Một con lắc đơn dao động theo phương trình li độ góc
α
7
sin
10
πt
(
α
tính bằng độ, t tính bằng s). Trong khoảng thời gian từ 0 đến 0,05s, độ lệch của dây treo so với phương thẳng đứng là
3
,
5
0
xảy ra vào thời điểm A. 0,0125s B. 0,0250s C. 0,0167s D. 0,0350s
Đọc tiếp
Một con lắc đơn dao động theo phương trình li độ góc α = 7 sin 10 πt ( α tính bằng độ, t tính bằng s). Trong khoảng thời gian từ 0 đến 0,05s, độ lệch của dây treo so với phương thẳng đứng là 3 , 5 0 xảy ra vào thời điểm
A. 0,0125s
B. 0,0250s
C. 0,0167s
D. 0,0350s
SGK Kết nối tri thức với cuộc sống - Trang 8
14 tháng 7 2023 lúc 22:57
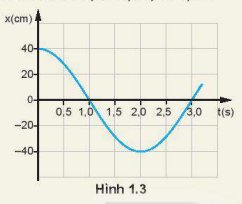
Đồ thị li độ - thời gian của một con lắc đơn dao động điều hoà được mô tả trên Hình 1.3.
1. Hãy mô tả dao động điều hoà của con lắc đơn.
2. Xác định biên độ và li độ của con lắc ở các thời điểm t = 0, t = 0,5 s ,t = 2,0 s.
tham khảo
1. Mô tả dao động điều hòa của con lắc đơn:
+ Tại thời điểm ban đầu t = 0, con lắc đơn đang ở vị trí biên dương (x = A = 40 cm) và sẽ dịch chuyển về vị trí cân bằng, con lắc đơn ở vị trí x = 0 khi t = 1 s.
+ Tại thời điểm t = 1 s, con lắc đơn bắt đầu chuyển động về phía biên âm và ở vị trí x = - A = - 40 cm khi t = 2 s.
+ Tại thời điểm t = 2 s, con lắc đang ở vị trí biên âm sẽ dịch chuyển về vị trí cân bằng và ở tại vị trí x = 0 khi t = 3 s.
2. Sử dụng thước kẻ để xác định li độ của con lắc tại các thời điểm.
Cách làm: Từ các thời điểm bài toán yêu cầu, dựng đường thẳng vuông góc với trục thời gian tại vị trí thời điểm đó, đường thẳng cắt đồ thị tại điểm nào thì ta kẻ đường thẳng song song với trục thời gian đi qua điểm cắt đó. Đường thẳng song song này cắt trục Ox tại điểm nào thì đó là li độ cần tìm.
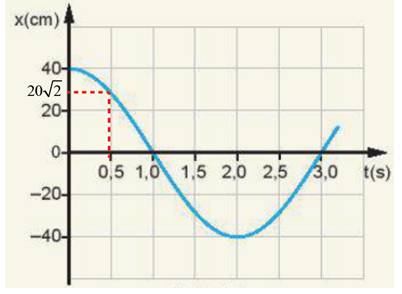
Tại thời điểm t = 0 vật bắt đầu xuất phát nên\(\left\{{}\begin{matrix}A=40cm\\x=40cm\end{matrix}\right.\)
Tại thời điểm t = 0,5 s: \(\left\{{}\begin{matrix}A=40cm\\x=20\sqrt{2}cm\end{matrix}\right.\)
Tại thời điểm t = 2,0 s, con lắc đang ở biên âm\(\left\{{}\begin{matrix}A=40cm\\x=-40cm\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Một con lắc đơn đang nằm yên ở vị trí cân bằng, dây treo có phương thẳng đứng. Truyền cho vật nặng một tốc độ
v
0
40cm/s theo phương ngang thì con lắc đơn dao động điều hòa. Biết rằng tại vị trí có li độ góc α thì nó có vận tốc v 20cm/s. Lấy g10
m
s
2
. Chọn gốc thời gian là lúc truyền vận tốc cho vật, chiều dương cùng chiều vận tốc ban đầu. Phương trình dao động của con l...
Đọc tiếp
Một con lắc đơn đang nằm yên ở vị trí cân bằng, dây treo có phương thẳng đứng. Truyền cho vật nặng một tốc độ v 0 = 40cm/s theo phương ngang thì con lắc đơn dao động điều hòa. Biết rằng tại vị trí có li độ góc α = thì nó có vận tốc v = 20cm/s. Lấy g=10 m s 2 . Chọn gốc thời gian là lúc truyền vận tốc cho vật, chiều dương cùng chiều vận tốc ban đầu. Phương trình dao động của con lắc theo li độ dài là
A. s = 8cos(5t + π/2)cm
B. s = 8cos(5t- π/2)cm
C. s = 5cos(8t + π/2)cm
D. s = 5cos(8t - π/2)cm
Một con lắc đơn dài l 1m dao động điều hoà tại một nơi có gia tốc trọng trường g 10m/s2 với biên độ 10cm. Lấy π2 10. Khi quả cầu ở vị trí có li độ góc α 40 thì tốc độ của quả cầu là A. 22,5cm/s B. 25,1cm/s C. 19,5cm/s D. 28,9cm/s
Đọc tiếp
Một con lắc đơn dài l = 1m dao động điều hoà tại một nơi có gia tốc trọng trường g = 10m/s2 với biên độ 10cm. Lấy π2 =10. Khi quả cầu ở vị trí có li độ góc α =40 thì tốc độ của quả cầu là
A. 22,5cm/s
B. 25,1cm/s
C. 19,5cm/s
D. 28,9cm/s
Góc lệch cực đại của con lắc là:
Chọn mốc tính thế năng ở vị trí cân bằng, ta áp dụng định luật bảo toàn cơ năng:
Đáp án A
Đúng 0
Bình luận (0)