Tìm số giao điểm của đồ thị hàm số y = x 3 + 2 x 2 − 4 x + 1 và đường thẳng y = 2.
A. 1.
B. 0.
C. 3.
D. 2.
Cho hàm số y=(1-2m)x+3 a) tìm m biết đồ thị hàm số đi qua điểm A(1;0) b) tìm m biết đồ thị hàm số đi qua điểm B(2;-4) c) tìm toạ độ giao điểm của 2 đồ thị hàm số ở câu a,b
a: Thay x=1 và y=0 vào (d), ta được:
1-2m+3=0
\(\Leftrightarrow m=2\)
Biết rằng đồ thị hàm số bậc 4: y = f(x) được cho như hình vẽ sau:
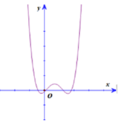
Tìm số giao điểm của đồ thị hàm số y = g(x) = [f’(x)]2 – f(x).f’’(x) và trục Ox
A. 0
B. 2
C. 4
D. 6
Đáp án A
Phương pháp:
Đặt Đáp án A
Phương pháp:
Đặt f(x) = a(x – x1)(x – x2)(x – x3)(x – x4), tính đạo hàm của hàm số y = f(x)
Xét hàm số h x = f ' x f x và chứng minh f(x).f’’(x) – [f’(x)]2 < 0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
Cách giải: Đồ thị hàm sốy = f(x) cắt trục hoành tại bốn điểm phân biệt nên
f(x) = a(x – x1)(x – x2)(x – x3)(x – x4)
=> f ’(x) = a(x – x1)(x – x2)(x – x3)(x – x4) + a(x – x1)(x – x3)(x – x4) + a(x – x1)(x – x2)(x – x4) + a(x – x1)(x – x2)(x – x3)
f ’(x) = f(x) 1 x - x 1 + 1 x - x 2 + 1 x - x 3 + 1 x - x 4 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4 => f’(x) ≠ 0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
Đặt h x = f ' x f x = 1 x - x 1 + 1 x - x 2 + 1 x - x 3 + 1 x - x 4 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
Ta có
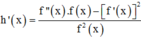
= - 1 ( x - x 1 ) 2 + - 1 ( x - x 2 ) 2 + - 1 ( x - x 3 ) 2 + - 1 ( x - x 4 ) 2 <0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
=> f ''(x).f(x) – [f’(x)]2 < 0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
=> g(x) = [f’(x)]2 – f(x).f’’(x)>0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
Khi f(x) = 0 => f '(x) ≠ 0 => g(x) = [f’(x)]2 – f(x).f’’(x) ≠ 0
Vậy đồ thị hàm số y = g(x) = [f’(x)]2 – f(x).f’’(x) không cắt trục Ox
Cho hàm số y=1/2 x^2 có đồ thị là (P) a) Vẽ đồ thị (P) của hàm số trên b) Tìm toạ độ giao điểm của (P) và đường thẳng (d) : y = x + 4
b: PTHĐGĐ là:
1/2x^2-x-4=0
=>x^2-2x-8=0
=>(x-4)(x+2)=0
=>x=4 hoặc x=-2
=>y=8 hoặc y=2
a: 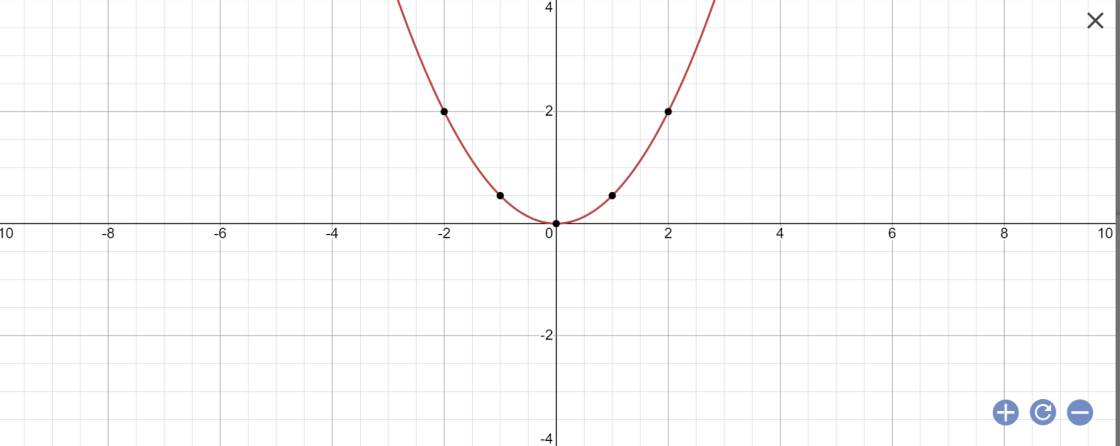
1/ Vẽ đồ thị hàm số : y = 3.|x| + x (1)
2/ Tìm tọa độ giao điểm đồ thị hàm số (1) với đường thẳng y=2
Cho hàm số y = ax2a) Xác định a để đồ thị của hàm số trên đi qua điểm A (4 ; 4).
b) Vẽ đồ thị của hàm số trên với a vừa tìm được và đồ thị của hàm số y = \(-\dfrac{1}{2}x\) trên cùng một mặt phẳng tọa độ Oxy.
c) Tìm tọa độ giao điểm của hai hàm số trên (câu b) bằng phép toán.
a) Để đồ thị hàm số \(y=ax^2\) đi qua điểm A(4;4) thì
Thay x=4 và y=4 vào hàm số \(y=ax^2\), ta được:
\(a\cdot4^2=4\)
\(\Leftrightarrow a\cdot16=4\)
hay \(a=\dfrac{1}{4}\)
a, - Thay tọa độ điểm A vào hàm số ta được : \(4^2.a=4\)
\(\Rightarrow a=\dfrac{1}{4}\)
b, Thay a vào hàm số ta được : \(y=\dfrac{1}{4}x^2\)
- Ta có đồ thì của hai hàm số :
c, - Xét phương trình hoành độ giao điểm :\(\dfrac{1}{4}x^2=-\dfrac{1}{2}x\)
\(\Leftrightarrow x^2+2x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
Vậy hai hàm số trên cắt nhau tại hai điểm : \(\left(0;0\right);\left(-2;1\right)\)
Cho hàm số y=f(x)=(m+1).|x|-3+m2
a) Tìm m để đồ thị hàm số đi qua A(-4;-3)
b) Với giá trị của m đã tìm ở câu a, hay tìm tọa độ giao điểm của đồ thị hàm số trên với:
+ Đồ thị hàm số y=-1
+ Với trục Ox
+ Với trục Oy
+Với đồ thị hàm số y=\(\frac{-1}{2}\)x
Nhanh, đúng, đủ => tick (giải trong ngày)
Bài 1 :
1, Viết phương trình đường thẳng đi qua hai điểm (1;2) và (-1;-4)
2, Tìm tọa độ giao điểm của đường thẳng trên truc tung và trục hoành
Bài 2 : Cho hàm số y=(m-2)x+m+3
1, Tìm điều kiện của m để hàm số luôn nghịch biến
2, Tìm m để đồ thị hàm số cắt trục tung tại điểm có hoành độ bằng 3
3, Tìm m để đồ thị hàm số trên và các đồ thị của các hàm số y=-x+2 ; y=2x-1 đồng quy
Bài 1: Cho hai hàm số bậc nhất: y= (k+1)x + 3 ; y= (3-2k)x + 1 a)Vẽ đồ thị của hai hàm số trên khi k=2 - Khi k=2 thì ta có hai hàm số : y= 3x+3 và y= -x+1 b) Tìm tọa độ giao điểm của đồ thị hàm số vừa vẽ. c) Tìm góc tạo bởi đường thẳng y= 3x+3 vớt trục Ox ( làm tròn đến phút ) giải giúp mik vs ak!! mik đang cần gấp lắm!!
a)
Thay x=0 vào hàm số y= 3x+3, ta được: y= 3 x 0 + 3 = 3
Thay y=0 vào hàm số y= 3x+3, ta được: 0= 3x+3 => x= -1
Vậy đồ thị hàm số đi qua điểm B(-1;0) và C(0;3)
Thay x=0 vào hàm số y= -x+1, ta được: y= -0 + 1 = 1
Thay y=0 vào hàm số y= -x+1, ta được: 0= -x+1 => x= 1
(Có gì bạn tự vẽ đồ thị nha :<< mình không load hình được sorry bạn nhiều)
b) Hoành độ giao điểm của hai đường thằng y=3x+3 và y=-x+1 :
3x+3 = -x+1
<=> 3x + x = 1 - 3
<=> 4x = -2
<=> x= - \(\dfrac{1}{2}\)
Thay x= - \(\dfrac{1}{2}\) vào hàm số y= -x+1, ta được: y= \(\dfrac{1}{2}\)+1 = \(\dfrac{3}{2}\)
Vậy giao điểm của hai đường thằng có tọa độ (\(-\dfrac{1}{2};\dfrac{3}{2}\))
c) Gọi góc tạo bởi đường thẳng y= 3x+3 là α
OB= \(\left|x_B\right|=\left|-1\right|=1\)
OC= \(\left|y_C\right|=\left|3\right|=3\)
Xét △OBC (O= 90*), có:
\(tan_{\alpha}=\dfrac{OC}{OB}=\dfrac{3}{1}=3\)
=> α= 71*34'
Vậy góc tạo bởi đường thằng y=3x+3 là 71*34'
Biết đồ thị hàm số bậc bốn y=f(x) được cho bởi hình vẽ bên dưới. Tìm số giao điểm của đồ thị hàm số y=g(x)= [f’(x)]2 – f(x). f’’(x) và trục hoành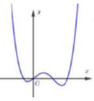
A. 4
B. 0.
C. 6.
D. 2.
Cho hàm số y=(m-2)x +m +2 .Tìm m để đồ thị hàm số đi qua giao điểm của đường thẳng y=3x-1 và y=x+3
giao diem co hoanh do la 3x-1=x+3=>x=2
toa do giao diem la A(2,5)
5=(m-2).2+m+2
5=2m-4+m+2=3m-2
3m=7
m=7/3