Đáp án B

Vì DA, DB,DC đôi 1 vuông góc, D khác O suy ra D đối xứng với O qua mp (ABC)

Mp (ABC) có dạng x+y+z+2=0

Suy ra D 

Trung điểm K (0;-1;-1) của BC

suy ra đường thẳng đi qua K và song song với AD có 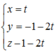   (d₁)

Trung điểm P  của AD

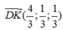
 suy ra đường thẳng đi qua P và song song với DK có ptđt 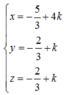   (d₂)

Tâm I là giao của d 1 , d 2  suy ra I   suy ra S=a+b+c=-1

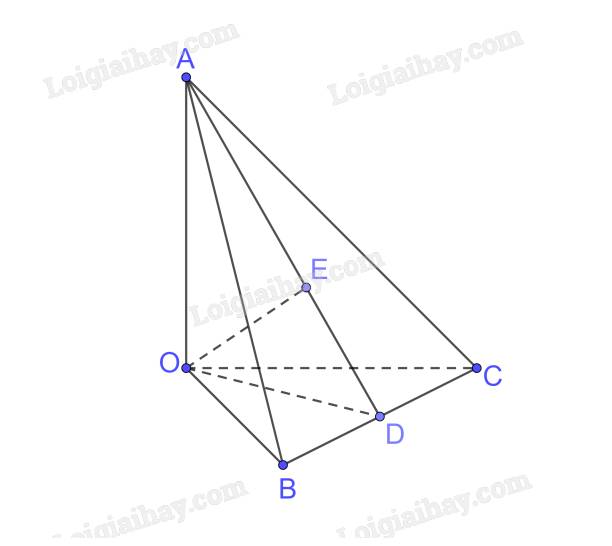
Ta có \(OA \bot OB,OA \bot OC \Rightarrow OA \bot \left( {OBC} \right);BC \subset \left( {OBC} \right) \Rightarrow OA \bot BC\)

Trong (OBC) kẻ \(OD \bot BC\)

\(\begin{array}{l} \Rightarrow BC \bot \left( {OAD} \right);BC \subset \left( {ABC} \right) \Rightarrow \left( {OAD} \right) \bot \left( {ABC} \right)\\\left( {OAD} \right) \cap \left( {ABC} \right) = AD\end{array}\)

Trong (OAD) kẻ \(OE \bot AD\)

\( \Rightarrow OE \bot \left( {ABC} \right) \Rightarrow d\left( {O,\left( {ABC} \right)} \right) = OE\)

Xét tam giác OBC vuông tại O có

\(\frac{1}{{O{D^2}}} = \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}} = \frac{1}{{{{\left( {a\sqrt 2 } \right)}^2}}} + \frac{1}{{{{\left( {2a} \right)}^2}}} = \frac{3}{{4{a^2}}} \Rightarrow OD = \frac{{2a\sqrt 3 }}{3}\)

Xét tam giác OAD vuông tại O có

\(\frac{1}{{O{E^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{D^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{{\left( {\frac{{2a\sqrt 3 }}{3}} \right)}^2}}} = \frac{7}{{4{a^2}}} \Rightarrow OE = \frac{{2a\sqrt 7 }}{7}\)

Vậy \(d\left( {O,\left( {ABC} \right)} \right) = \frac{{2a\sqrt 7 }}{7}\)

                           Bài làm :

a) Ta có :

\(\widehat{ACB}\text{ là góc nội tếp chắn nửa đường tròn}\)

\(\Rightarrow\widehat{ACB}=90^o\Rightarrow\widehat{ACM}=180^o-\widehat{ACB}=90^o\)

Từ đó ; ta có :

\(\widehat{ACM}+\widehat{AHM}=90+90=180^o\)

=> Tứ giác AHMC là tứ giác nội tiếp đường tròn vì có 2 góc đối diện  = 180 độ 

=> Điều phải chứng minh

b) Theo phần a : Tứ giác AHMC là tứ giác nội tiếp 

\(\Rightarrow\widehat{AMH}=\widehat{ACH}\left(1\right)\)

Xét đường tròn (O) : Góc ADC và góc ABC đều là 2 góc nội tiếp cùng chắn cung AC

\(\Rightarrow\widehat{ADC}=\widehat{ABC}\left(2\right)\)

Vì CD⊥AB ; MH⊥AB

=> CD//MH 

=>∠ADC = ∠AMH ( 2góc so le trong ) (3)

Từ (1) ; (2) ; (3) 

\(\Rightarrow\widehat{ABC}=\widehat{ACH}\)

=> Điều phải chứng minh

c)∠AOC = 45^o

=>∠COB = 180 - 45 = 135^o

\(\Rightarrow S_{OCB}=\frac{\pi.R^2.n}{360}=\frac{\pi.2^2.135}{360}=\frac{3}{2}\pi\left(cm^2\right)\)

a) Xét tứ giác AHMC có 

góc ACM + góc AHM = 180 độ

Vậy tứ giác AHMC nội tiếp

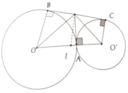
a, Chứng minh được tương tự câu 1a,

=>  O ' M O ^ = 90 0  

Áp dụng hệ thức lượng trong tam giác vuông tính được MA =  R r

b, Chứng minh  S B C O O ' = R + r R r

c, Chứng minh được: ∆BAC:∆OMO’ =>  S B A C S O M O ' = B C O O ' 2

=>  S B A C = S O M O ' . B C 2 O O ' 2 = 4 R r R r R + r

d, Tứ giác OBCO’ là hình thang vuông tại B và C có IM là đường trung bình => IM ⊥ BC = {M}

Chọn D

Từ giả thiết suy ra: ΔABC cân tại A có:

Gọi I là trung điểm của BC  ⇒ A I ⊥ B C

Giả sử H là trực tâm của tam giác ABC.

Ta thấy  O A ⊥ O B C

Vì  O B ⊥ O A C ⇒ O B ⊥ A C và  A C ⊥ B H nên  A C ⊥ O B H ⇒ O H ⊥ A C   ( 1 )

B C ⊥ O A I ⇒ O H ⊥ B C   ( 2 )

Từ (1) và (2) suy ra  O H ⊥ A B C

Có  O I = 1 2 B C = a 2 2 = O A

=> ΔAOI vuông cân tại O => H là trung điểm AI và  O H = 1 2 A I = a 2

Khi đó:

Đáp án D

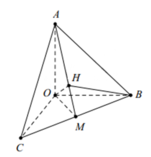
Gọi M là trung điểm của  B C ⇒ B M ⊥ O A M

Vì  O H ⊥ A B C ⇒ 1 O H 2 = 1 O A 2 + 1 O B 2 + 1 O C 2 ⇒ O H = a 2

Tam giác OAH vuông tại H, có  A H = O A 2 − O H 2 = a 2

Diện tích tam giác vuông OAH là  S Δ O A H = 1 2 . O H . A H = a 2 8

Thể tích khối chóp OABH là  

V O A B H = 1 3 . B M . S Δ O A H = 1 3 . a 2 2 . a 2 8 = a 3 2 48