Biết rằng α ; β là các số thực thỏa mãn 2 β 2 α + 2 β = 8 2 - α + 2 - β . Giá trị của α + 2 β bằng
A. 1
B. 2
C. 4
D. 3
Cho góc nhọn α biết rằng cos α - sin α = 1/3 . Giá trị của sin α .cos α là
A. 2 3
B. 3 2
C. 4 9
D. 9 4
Dựng góc nhọn α , biết rằng: cos α = 0,75 tg α = 1
*Cách dựng:
- Dựng góc vuông xOy
- Trên tia Ox dựng đoạn OA bằng 3 đơn vị dài
- Dựng cung tròn tâm A bán kính 4 đơn vị dài và cắt Oy tại B
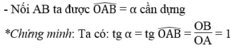
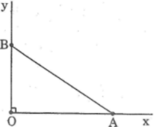
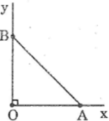
Dựng góc nhọn α , biết rằng: sin α = 0,25
sin α = 0,25 = 14
*Cách dựng: hình a
- Dựng góc vuông xOy
- Trên tia Ox dựng đoạn OA bằng 1 đơn vị dài
- Dựng cung tròn tâm A bán kính 4 đơn vị dài và cắt Oy tại B
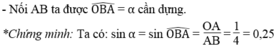
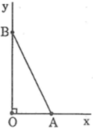
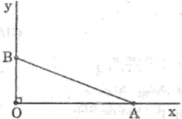
Dựng góc nhọn α , biết rằng: sin cotg α = 2
*Cách dựng: hình d
- Dựng góc vuông xOy
- Trên tia Ox dựng đoạn OA bằng 2 đơn vị dài
- Trên tia Oy dựng đoạn OB bằng 1 đơn vị dài
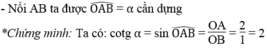
Biết rằng α , β là các số thực thỏa mãn 2 β 2 α + 2 β = 8 2 - α + 2 - β . Giá trị của α + 2 β
A. 1
B. 2
C. 4
D. 3
Cho biết 0≤α≤π20≤α≤π2 sao cho
sin3(α)+cos3(α)=1sin3(α)+cos3(α)=1
Và β=sin(α)+cos(α)β=sin(α)+cos(α)
a) Tính ∑α=07π2(sin−1(β)+α)∑α=07π2(sin−1(β)+α)
b) Chứng minh rằng số ββ thỏa đề bài là nghiệm của phương trình: β3−6β+5=0
Cho 2 hàm số f ( x ) = x 2 và g ( x ) = x 1 2 . Biết rằng α > 0, f(α) < g(α). Khẳng định nào sau đây là đúng?
A. 0 < α < 1/2
B. 0 < α < 1
C. 1/2 < α < 2
D. α > 1
Cho tam giác ABC, phân giác AD (D ∈ BC). Biết rằng ∠A = α, AC = b, AB = c. Tính AD theo α, b, c.
A2+AD⋅b⋅sinA2" role="presentation" style="border:0px; box-sizing:inherit; direction:ltr; display:inline-block; float:none; font-size:18.08px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
A2(b+c)" role="presentation" style="border:0px; box-sizing:inherit; direction:ltr; display:inline-block; float:none; font-size:18.08px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
2bc⋅cosαb+c" role="presentation" style="border:0px; box-sizing:inherit; direction:ltr; display:inline-block; float:none; font-size:18.08px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml"> (dpcm)
a) Xét tam giác HAB và tam giác ABC có:
Góc AHB= góc BAC (= 900 )
B> là góc chung
⇒ tam giác HAB ~ tam giác ABC (g.g)
b) Xét ΔΔ ABC vuông tại A: BC2 = AB2 + AC2
Hay BC2 = 122 + 162
BC2 = 144 + 256 = 400
=> BC = √400 = 20 (cm)
Ta có : Δ HAB ∼ Δ ABC
=>
Hay
=> AH = cm
c)
Ta có
DE là tia phân giác của góc ADB trong tam giác DAB,
áp dụng t/c tia phân giác thì
DG là tia phân giác cảu góc CDA trong tam giác CDA.
áp dụng t/c tia phân giác thì
VẬy (dpcm)
Tính góc A của tam giác ABC biết rằng các đường phân giác BD, CE cắt nhau tại I trong đó góc BIC bằng: α (α > 90o)
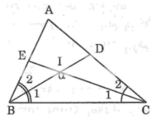
Trong ΔBIC có: ∠(BIC) + ∠B1 + ∠C1 = 180o (tổng 3 góc trong tam giác)
Suy ra: ∠B1 + ∠C1 = 180o - ∠(BIC)
Ta có:
∠B1 = 1/2 ∠B (vì BD là tia phân giác)
∠C1 = 1/2 ∠C (vì CE là tia phân giác)
Suy ra: ∠B + ∠C = 2(∠B1 + ∠C1) = 2.(180o - ∠(BIC))
Trong ΔABC có: ∠A + ∠B + ∠C = 180o (tổng ba góc trong tam giác)
Suy ra: ∠A = 180o - (∠B + ∠C) = 180o - 2.(180o - ∠(BIC)) = 2. ∠(BIC) – 180o
∠(BIC) = α thì ∠A = 2.α – 180o.