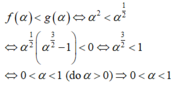Các câu hỏi tương tự
Đường thẳng x α ( α là số thực dương) cắt đồ thị các hàm số
y
f
(
x
)
x
1
4
và
y
g
(
x
)
x
1
5
lần lượt tại hai điểm A và B. Biết rằng tung độ điểm A bé hơn tung độ điểm B. Khẳng định nào sau đây là đúng? A. 0 α 1 B. α 1 C. 1/5 α 4 D. 1/4 α 5
Đọc tiếp
Đường thẳng x = α ( α là số thực dương) cắt đồ thị các hàm số y = f ( x ) = x 1 4 và y = g ( x ) = x 1 5 lần lượt tại hai điểm A và B. Biết rằng tung độ điểm A bé hơn tung độ điểm B. Khẳng định nào sau đây là đúng?
A. 0 < α < 1
B. α > 1
C. 1/5 < α < 4
D. 1/4 < α < 5
Xét các khẳng định sau i) Nếu hàm số y f(x) xác định trên [-1;1] thì tồn tại
α
∈
-
1
;
1
thỏa mãn
f
(
x
)
≥
f
(
α
)
∀
x
∈
-
1
;
1
. ii) Nếu hàm số y f(x) xác định trên [-1;1] thì tồn...
Đọc tiếp
Xét các khẳng định sau
i) Nếu hàm số y = f(x) xác định trên [-1;1] thì tồn tại α ∈ - 1 ; 1 thỏa mãn f ( x ) ≥ f ( α ) ∀ x ∈ - 1 ; 1 .
ii) Nếu hàm số y = f(x) xác định trên [-1;1] thì tồn tại β ∈ - 1 ; 1 thỏa mãn f ( x ) ≤ f ( β ) ∀ x ∈ - 1 ; 1 .
iii) Nếu hàm số y = f(x) xác định trên [-1;1] thỏa mãn f(-1).f(1)<0 thì tồn tại γ ∈ - 1 ; 1 thỏa mãn f ( γ ) = 0
Số khẳng định đúng là
A. 3.
B. 2.
C. 1.
D. 0.
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng và mặt phẳng
(
α
)
: x+3y+z+10 .Khẳng định nào sau đây là đúng?
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng 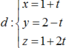 và mặt phẳng
(
α
)
: x+3y+z+1=0 .Khẳng định nào sau đây là đúng?
và mặt phẳng
(
α
)
: x+3y+z+1=0 .Khẳng định nào sau đây là đúng?
![]()

Tính khoảng cách giữa hai mặt phẳng (α) và (β) cho bởi các phương trình sau đây:
(α): x – 2 = 0
(β): x – 8 = 0.
Cho điểm M(1; 4; 2) và mặt phẳng (α): x + y + z – 1 = 0. Tính khoảng cách từ M đến mp(α).
Cho
P
:
x
+
y
-
z
-
1
0
và
Q
:
-
2
x
+
z
+
4
0
và
A
-
1
;
1
;
3
. Gọi
α
là mặt phẳng qua...
Đọc tiếp
Cho P : x + y - z - 1 = 0 và Q : - 2 x + z + 4 = 0 và A - 1 ; 1 ; 3 . Gọi α là mặt phẳng qua A, α ⊥ P , α ⊥ Q . Tìm một vectơ pháp tuyến n → của α .
![]()
![]()
![]()
![]()
Cho điểm M(2; 1; 0) và mặt phẳng (α): x + 3y – z – 27 = 0. Tìm tọa độ điểm M' đối xứng với M qua (α).
Trong không gian Oxyz cho điểm M(2;1;1) mặt phẳng
α
: x+y+z-40 và mặt cầu (S):
x
-
3
2
+
(
y
-
3
)
2
+
(
z
-...
Đọc tiếp
Trong không gian Oxyz cho điểm M(2;1;1) mặt phẳng α : x+y+z-4=0 và mặt cầu (S): x - 3 2 + ( y - 3 ) 2 + ( z - 4 ) 2 = 16 Phương trình đường thẳng α đi qua M và nằm trong α cắt mặt cầu (S) theo một đoạn thẳng có độ dài nhỏ nhất. Đường thẳng α đi qua điểm nào trong các điểm sau đây?
![]()
![]()
![]()
![]()
Cho α là một số thực và hàm số
y
1
x
1
-
2
α
α
đồng biến trên (0; +∞). Khẳng định nào sau đây là đúng A. α 1 B.
0
α
1
2
C. ...
Đọc tiếp
Cho α là một số thực và hàm số y = 1 x 1 - 2 α α đồng biến trên (0; +∞). Khẳng định nào sau đây là đúng
A. α < 1
B. 0 < α < 1 2
C. 1 2 < α < 1
D. α > 1