Số mặt phẳng đối xứng của hình lập phương A B C D . A ' B ' C ' D ' là
A. 3
B. 6
C. 9
D. 12
Cho hình lập phương có cạnh bằng a và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi S 1 là diện tích 6 mặt của hình lập phương, S 2 là diện tích xung quanh của hình trụ. Tỉ số S 2 / S 1 bằng:
A. π /6 B. 1/2
C. π /2 D. π
Trong mặt phẳng Oxy, cho hai điểm I(1; 2), M(-2; 3), đường thẳng d có phương trình 3x – y + 9 = 0 và đường tròn (C) có phương trình: x 2 + y 2 + 2 x − 6 y + 6 = 0 .
Hãy xác định tọa độ của điểm M’, phương trình của đường thẳng d’ và đường tròn (C’) theo thứ tự là ảnh của M, d và (C) qua
a) Phép đối xứng qua gốc tọa độ;
b) Phép đối xứng qua tâm I.
a) Gọi M', d' và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua O.
Dùng biểu thức tọa độ của phép đối xứng qua gốc tọa độ ta có :
M′ = (2; −3), phương trình của d′: 3x – y – 9 = 0, phương trình của đường tròn (C′): x 2 + y 2 − 2 x + 6 y + 6 = 0 .
b) Gọi M', d' và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua I .
Vì I là trung điểm của MM' nên M′ = (4;1)
Vì d' song song với d nên d' có phương trình 3x – y + C = 0.
Lấy một điểm trên d, chẳng hạn N(0; 9).
Khi đó ảnh của N qua phép đối xứng qua tâm I là N′(2; −5).
Vì N' thuộc d nên ta có 3.2 − (−5) + C = 0. Từ đó suy ra C = -11.
Vậy phương trình của d' là 3x – y – 11 = 0.
Để tìm (C'), trước hết ta để ý rằng (C) là đường tròn tâm J(−1; 3),
bán kính bằng 2. Ảnh của J qua phép đối xứng qua tâm I là J′(3; 1).
Do đó (C') là đường tròn tâm J' bán kính bằng 2. Phương trình của (C') là x − 3 2 + y − 1 2 = 4 .
Cho hình lập phương ABCD.A′B′C′D′ABCD.A′B′C′D′ cạnh aa và một điểm MM trên cạnh AB,AM=x,0<x<aAB,AM=x,0<x<a. Xét mặt phẳng (PP) đi qua điểm MM và chưa đường chéo A′C′A′C′ của hình vuông A′B′C′D′.A′B′C′D′.
1.1. Tính diện tích của thiết diện của hình lập phương cắt bởi mặt phẳng (PP).
2.2. Mặt phẳng (PP) chia hình lập phương thành hai khối đã diện. Hãy tìm xx để thể tích của một trong hai khối đa diện đó gấp đôi thể tích của khối đa diện kia.
Câu 13: Tổng a – (–b + c – d) bằng:
A. a– b+ c – d B. a+ b+ c+ d C. a+ b+ c – d D. a+ b – c+ d
Câu 16: Hình vuông có:
A.4 trục đối xứng B.3 trục đối xứng C.2 trục đối xứng D.1 trục đối xứng
Câu 13: Tổng a – (–b + c – d) bằng:
A. a– b+ c – d B. a+ b+ c+ d C. a+ b+ c – d D. a+ b – c+ d
Câu 16: Hình vuông có:
A.4 trục đối xứng B.3 trục đối xứng C.2 trục đối xứng D.1 trục đối xứng
Câu 13: Tổng a – (–b + c – d) bằng:
A. a– b+ c – d B. a+ b+ c+ d C. a+ b+ c – d D. a+ b – c+ d
Câu 16: Hình vuông có:
A.4 trục đối xứng B.3 trục đối xứng C.2 trục đối xứng D.1 trục đối xứng
Trên mặt phẳng (α) cho hình vuông ABCD. Các tia Ax, By, Cz, Dt vuông góc với mặt phẳng (α) và nằm về một phía đối với mặt phẳng (α). Một mặt phẳng (β) lần lượt cắt Ax, By, Cz, Dt tại A', B', C', D'.
a) Tứ giác A', B', C', D' là hình gì? Chứng minh rằng .
b) Chứng minh rằng điều kiện để tứ giác A', B', C', D' là hình thoi là nó có hai đỉnh đối diện cách đều mặt phẳng (α).
c) Chứng minh rằng điều kiện để tứ giác A', B', C', D' là hình chữ nhật là nó có hai đỉnh kề nhau cách đều mặt phẳng (α).
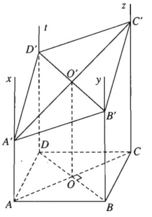
a) Ta có hai mặt phẳng song song là: (Ax, AD) // (By, BC)
Hai mặt phẳng này bị cắt bởi mặt phẳng (β) nên ta suy ra các giao tuyến của chúng phải song song nghĩa là A′D′ // B′C′.
Tương tự ta chứng minh được A′B′ // D′C′. Vậy A', B', C', D' là hình bình hành. Các hình thang AA'C'C và BB'D'D đều có OO' là đường trung bình trong đó O là tâm của hình vuông ABCD và O' là tâm của hình bình hành A',B',C',D'. Do đó: AA′ + CC′ = BB′ + DD′ = 2OO′
b) Muốn hình bình hành A',B',C',D' là hình thoi ta cần phải có A'C' ⊥ B'D'. Ta đã có AC ⊥ BD. Người ta chứng minh được rằng hình chiếu vuông góc của một góc vuông là một góc vuông khi và chỉ khi góc vuông đem chiếu có ít nhất một cạnh song song với mặt phẳng chiếu hay nằm trong mặt chiếu. Vậy A', B', C', D' là hình thoi khi và chỉ khi A'C' hoặc B'D' song song với mặt phẳng (α) cho trước. Khi đó ta có AA' = CC' hoặc BB' = DD'.
c) Muốn hình bình hành A', B', C', D' là hình chữ nhật ta cần có A'B' ⊥ B'C', nghĩa là A'B' hoặc B'C' phải song song với mặt phẳng (α)(α). Khi đó ta có AA' = BB' hoặc BB' = CC', nghĩa là hình bình hành A', B', C', D' có hai đỉnh kề nhau cách đều mặt phẳng (α) cho trước.
Cho hình lập phương ABCD.A'B'C'D'. Tính tan của góc giữa hai mặt phẳng (A'BC) và (A'B'C'D')?
Cho hai số phức α = a + bi, β = c + di. Hãy tìm điều kiện của a, b, c, d để các điểm biểu diễn α và β trên mặt phẳng tọa độ:
a) Đối xứng với nhau qua trục Ox ;
b) Đối xứng với nhau qua trục Oy;
c) Đối xứng với nhau qua đường phân giác của góc phần tư thứ nhất và góc phần tư thứ ba;
d) Đối xứng với nhau qua gốc tọa độ.
a) a = c, b = - d
b) a = -c, b = d
c) a = d, b = c
d) a = -c, b = - d
Trong không gian Oxyz, cho \(S\left(0;0;2\right),A\left(0;0;0\right),B\left(1;2;0\right),C\left(0;2;0\right)\)
a) Viết phương trình của mặt phẳng (P) đi qua A và vuông góc với SB
b) Tìm tọa độ của các điểm B' là giao của (P) với đường thẳng SB, C' là giao của (P) với đường thẳng SC
c) Tính thể tích tứ diện SAB'C
d) Tìm điểm đối xứng với B qua mặt phẳng (P)
e) Chứng minh các điểm A, B, C, B', C' cùng thuộc một mặt cầu. Viết phương trình của các mặt cầu đó và phương trình của mặt phẳng tiếp xúc với mặt cầu đó tại C'
Trong không gian Oxyz, cho bốn điểm A(3;4;-2), B(1;0;-1), C(3;0;3), D(4;-1;1)
a) Viết phương trình mặt phẳng trung trực của đoạn thẳng AB
b)Viết phương trình mặt phẳng(ABC).CM ABCD là một tứ diện.Tính khoảng cách từ điểm D đến mặt phẳng (ABC)
c) Tìm tọa độ điểm D' đối xứng với điểm D qua mặt phẳng (ABC)
d) Viết PT mặt cầu (S) ngoại tiếp tứ diện ABCD
Trong không gian Oxyz, cho ba điểm A 2 ; 0 ; 0 , B 0 ; 2 ; 0 , C 0 ; 0 ; 2 và D là điểm đối xứng của gốc tọa độ O qua mặt phẳng (ABC). Điểm I(a,b,c) là tâm mặt cầu đi qua bốn điểm A; B; C; D. Tính giá trị của biểu thức P = a + 2 b + 3 c
A. P = 0
B. P = 2
C. P = -2
D. P = 1