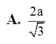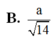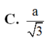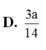Cho hình lập phương A B C D . A ' B ' C ' D ' cạnh a. Tính khoảng cách từ điểm A đến mặt phẳng (A'BC) theo a.
A. a 2 2
B. a 3 3
C. a 3 2
D. a 2 3
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Chứng minh rằng các khoảng cách từ các điểm B, C, D, A', B' và D' đến đường chéo AC' đều bằng nhau. Tính khoảng cách đó.
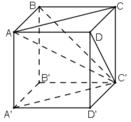
a) Ta có: ∆ ABC’ = ∆ C’CA = ∆ADC’=∆ AA’C’ =∆ C’B’A = ∆C’D’A (c.c.c)
⇒ Các đường cao hạ từ B; C; D; A’; B’; D’ xuống AC’ bằng nhau
( chú ý: các tam giác trên đều có chung cạnh AC’)
Gọi khoảng cách đó là h.
Ta có: CC’ = a; 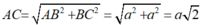
ΔC’AC vuông tại C, có hai cạnh góc vuông là CA và CC’. Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có:
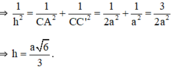
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Chứng minh rằng các khoảng cách từ điểm B, C, D, A', B', D' đến đường chéo AC' đều bằng nhau. Tính khoảng cách đó ?
Cho hình lập phương ABCD.A′B′C′D′ cạnh a. Khoảng cách từ điểm A đến mặt phẳng (A′B′CD) bằng
A. a 2
B. 3 a
C. 3 3 a
D. 2 2 a
Gọi O là tâm của hình vuông
A D D ' A ' ⇒ A O ⊥ A ' B ' C D ⇒ d A , A ' B ' C D = A O = 2 a 2
Chọn đáp án D.
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Chứng minh rằng khoảng cách từ các điểm A', B, D; C, B', D tới đường chéo AC' bằng nhau. Tính khoảng cách đó.
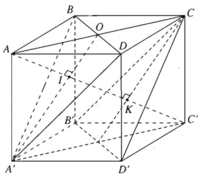
Điểm A cách đều ba đỉnh của tam giác đều A'BD vì ta có AB = AD = AA′ = a, điểm C' cũng cách đều ba đỉnh của tam giác đều đó vì ta có:
C′B = C′D = C′A′ = a√2
Vậy AC' là trục của đường tròn ngoại tiếp tam giác A'BD, tức là đường thẳng AC' vuông góc với mặt phẳng (A'BD) tại trọng tâm I của tam giác A'BD. Ta cần tìm khoảng cách A'I.
Ta có A′I = BI = DI = 2A′O/3 với O là tâm của hình vuông ABCD
Ta lại có 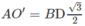
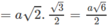
Vậy 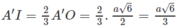
Tương tự điểm C' cách đều ba đỉnh của tam giác đều CB'D', tính được khoảng cách từ C, B', D' tới đường chéo AC'.
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Chứng minh rằng khoảng cách từ các điểm A', B, D; C, B', D' tới đường chéo AC' bằng nhau. Tính khoảng cách đó ?
Điểm A cách đều ba đỉnh, của tam giác đều A'BD vì ta có AB = AD = AA' = a, điểm C' cũng cách đều ba đỉnh của tam giác đều đó vì ta có :
\(C'B=C'D=C'A'=a\sqrt{2}\)

Bài 1. Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 4. a. Tính độ dài đường chéo của hình lập phương. b. Tính góc giữa AC' và mặt đáy c. Tính góc giữa AC và B'C' d. Tính khoảng cách từ A đến (A'BD)
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1 . Tính khoảng cách d từ điểm A đến mp (BDA')
Giải chi tiết:

Dễ thấy, tứ diện A.A′BD�.�′�� có ba cạnh AB,AD,AA′��,��,��′ đôi một vuông góc.
Đặt d=d(A,(A′BD))�=�(�,(�′��)) ta có :
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA = a\) (Hình 78).
a) Tính khoảng cách từ điểm \(S\) đến đường thẳng \(C{\rm{D}}\).
b) Tính khoảng cách từ điểm \(D\) đến mặt phẳng \(\left( {SAB} \right)\).
c) Tính khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SCD} \right)\).
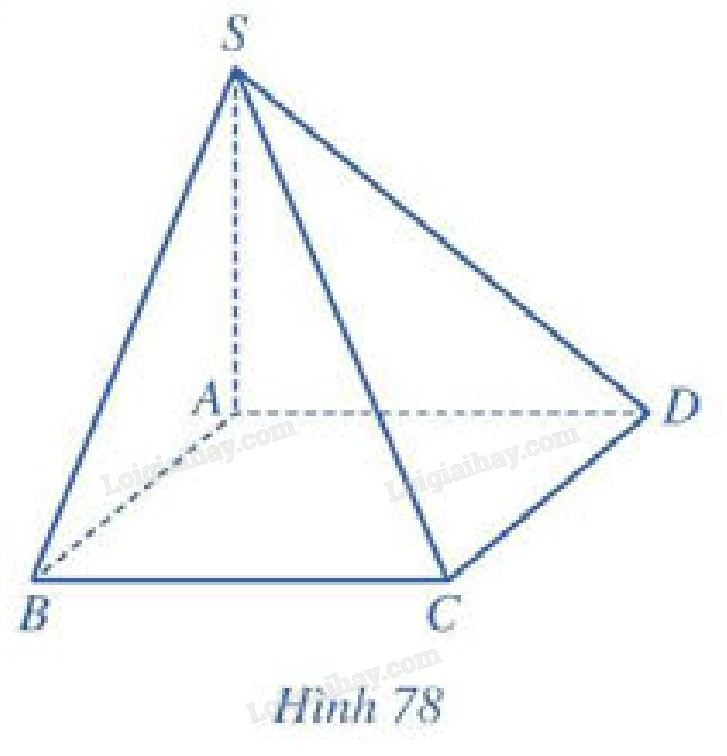
a) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot C{\rm{D}}\)
\(ABCD\) là hình vuông \( \Rightarrow A{\rm{D}} \bot C{\rm{D}}\)
\(\begin{array}{l} \Rightarrow C{\rm{D}} \bot \left( {SA{\rm{D}}} \right) \Rightarrow C{\rm{D}} \bot S{\rm{D}}\\ \Rightarrow d\left( {S,C{\rm{D}}} \right) = S{\rm{D}} = \sqrt {S{A^2} + A{{\rm{D}}^2}} = a\sqrt 2 \end{array}\)
b) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot A{\rm{D}}\)
\(ABCD\) là hình vuông \( \Rightarrow A{\rm{B}} \bot A{\rm{D}}\)
\( \Rightarrow A{\rm{D}} \bot \left( {SA{\rm{B}}} \right) \Rightarrow d\left( {D,\left( {SAB} \right)} \right) = A{\rm{D}} = a\)
c) Kẻ \(AH \bot S{\rm{D}}\left( {H \in S{\rm{D}}} \right)\).
\(C{\rm{D}} \bot \left( {SA{\rm{D}}} \right) \Rightarrow C{\rm{D}} \bot AH\)
\( \Rightarrow AH \bot \left( {SC{\rm{D}}} \right) \Rightarrow d\left( {A,\left( {SC{\rm{D}}} \right)} \right) = AH\)
Tam giác \(SAD\) vuông tại \(A\) có đường cao \(AH\)
\( \Rightarrow AH = \frac{{SA.A{\rm{D}}}}{{S{\rm{D}}}} = \frac{{a\sqrt 2 }}{2}\)
Vậy \(d\left( {A,\left( {SC{\rm{D}}} \right)} \right) = \frac{{a\sqrt 2 }}{2}\).
Cho hình lập phương A B C D . A ’ B ’ C ’ D ’ có cạnh bằng a. Gọi I là điểm thuộc cạnh AB sao cho AI = a. Tính khoảng cách từ điểm C đến mặt phẳng ( B ’ D I ) .
A . 2 a 3
B . a 14
C . a 3
D . 3 a 14
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi I là điểm thuộc cạnh AB sao cho AI=a. Tính khoảng cách từ điểm C đến mặt phẳng (B'DI).