Giải chi tiết:

Dễ thấy, tứ diện A.A′BD�.�′�� có ba cạnh AB,AD,AA′��,��,��′ đôi một vuông góc.
Đặt d=d(A,(A′BD))�=�(�,(�′��)) ta có :
Giải chi tiết:

Dễ thấy, tứ diện A.A′BD�.�′�� có ba cạnh AB,AD,AA′��,��,��′ đôi một vuông góc.
Đặt d=d(A,(A′BD))�=�(�,(�′��)) ta có :
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1. Khoảng cách từ điểm A đến mặt phẳng bằng (A'BD)
A. 3
B. 3
C. 2 2
D. 3 3
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Chứng minh rằng các khoảng cách từ các điểm B, C, D, A', B' và D' đến đường chéo AC' đều bằng nhau. Tính khoảng cách đó.
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Chứng minh rằng khoảng cách từ các điểm A', B, D; C, B', D tới đường chéo AC' bằng nhau. Tính khoảng cách đó.
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách giữa hai đường thẳng AB, C'D' bằng
A. a
B. a 2
C. a 3
D. a 3 2
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi I là điểm thuộc AB sao cho AI = a 3 . Tính khoảng cách từ điểm C đến (B’DI).
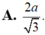
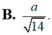
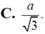
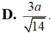
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách giữa hai đường thẳng BB ' và AC ' bằng:
![]()
![]()
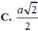
![]()
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách giữa hai đường thẳng AA' và B'C bằng:
A . a 3
B . a 3 2
C . a
D . a 3 3
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Khoảng cách giữa hai đường thẳng BD và A'D' bằng
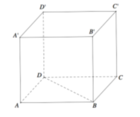
A. a 2 2
B. a.
C. a 2
D. a 3
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a.
a) Hãy xác định đường vuông góc chung của hai đường thẳng chéo nhau BD' và B'C.
b) Tính khoảng cách của hai đường thẳng BD' và B'C