Cho hai số thực x, y thay đổi thỏa mãn điều kiện x 2 + y 2 = 2 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = 2 ( x 3 + y 3 ) - 3 x y . Giá trị của của M + m bằng
A. -4
B. - 1 2
C. -6
D. 1 - 4 2
Bài 1 :Cho 2 số dương x,y thỏa mãn điều kiện \(x+y\le1\). Chứng minh\(x^2-\frac{3}{4x}-\frac{x}{y}\le\frac{-9}{4}\)
Bài 2 : Cho 2 số thực x,y thay đổi thỏa mãn điều kiện x+y\(\ge1\)và x>0
Tìm giá trị nhỏ nhất của biểu thức \(M=y^2+\frac{8x^2+y}{4x}\)
bài 3: cho 3 số dương x,y,z thay đổi luôn thỏa mãn điều kiện x+y+z=1. Tìm giá trị lớn nhất của biểu thức:\(P=\dfrac{x}{x+1}+\dfrac{y}{y+1}+\dfrac{z}{z+1}\)
3: \(P=\dfrac{x}{\left(x+y\right)+\left(x+z\right)}+\dfrac{y}{\left(y+z\right)+\left(y+x\right)}+\dfrac{z}{\left(z+x\right)+\left(z+y\right)}\le\dfrac{1}{4}\left(\dfrac{x}{x+y}+\dfrac{x}{x+z}\right)+\dfrac{1}{4}\left(\dfrac{y}{y+z}+\dfrac{y}{y+x}\right)+\dfrac{1}{4}\left(\dfrac{z}{z+x}+\dfrac{z}{z+y}\right)=\dfrac{3}{2}\).
Đẳng thức xảy ra khi x = y = x = \(\dfrac{1}{3}\).
Cho hai số thực x,y thay đổi thỏa mãn các điều kiện x+y≥1 và 0<x<1. Tìm GTNN của biểu thức A=\(\frac{8x^2+y}{4x}+y^2\)
Cho hai số thực x≠0, y≠0 thay đổi và thỏa mãn điều kiện (x+y).xy=x2+y2–xy. Giá trị lớn nhất của biểu thức M = 1 x 3 + 1 y 3 là
A. 18
B. 1
C. 9
D. 16
Đáp án D
Phương pháp giải:
Đặt ẩn phụ, đưa về hàm một biến, dựa vào giả thiết để tìm điều kiện của biến
Lời giải:
Từ giả thiết chia cả 2 vế cho x2y2 ta được : 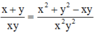
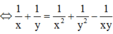
Đặt 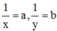 ta có
ta có ![]()
Khi đó ![]()
![]()
Ta có ![]() mà
mà 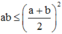
nên ![]()
![]()
![]()
Dấu đẳng thức xảy ra khi 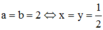 . Vậy Mmax = 16
. Vậy Mmax = 16
\(\text{Các số thực không âm x,y,z thay đổi thỏa mãn điều kiện: x^2+ y^2+x^2+x^2y^2+y^2z^2+z^2x^2=6. \text{Tìm giá trị lớn nhất và nhỏ nhất của biểu thức Q=x+y+z}}\)\(\text{Các số thực không âm x,y,z thay đổi thỏa mãn điều kiện x^2+y^2+z^2+x^2y^2+y^2z^2+z^2x^2=6. Tìm giá trị lớn nhất và nhỏ nhất của biểu thức Q=x+y+z}\)
https://diendantoanhoc.net/topic/182493-%C4%91%E1%BB%81-thi-tuy%E1%BB%83n-sinh-v%C3%A0o-l%E1%BB%9Bp-10-%C4%91hsp-h%C3%A0-n%E1%BB%99i-n%C4%83m-2018-v%C3%B2ng-2/
bài này năm trrong đề thi tuyển sinh vào lớp 10 ĐHSP Hà Nội Năm 2018 (vòng 2) bn có thể tìm đáp án trên mạng để tham khảo
Sử dụng bất đẳng thức AM-GN, ta có:
\(x^2y^2+1\ge2xy,\) \(y^2z^2+1\ge2yz,\) \(z^2x^2+1\ge2zx\)
Cộng các bất đẳng thức trên lại theo vế, sau đó cộng hai vế của bất đẳng thức thu được với \(x^2+y^2+z^2\), ta được:
\(\left(x+y+z\right)^2\le x^2+y^2+z^2+x^2y^2+y^2z^2+z^2x^2+3=9\)
Từ đó suy ra: \(Q\le3\)
Mặt khác, dễ thấy dấu bất đẳng thức xảy ra khi \(x=y=z=1\) nên ta có kết luận \(Max_Q=3\)
Ta sẽ chứng minh \(Q\ge\sqrt{6}\) với dấu đẳng thức xảy ra, chẳng hạn \(x=\sqrt{6},\) \(y=z=0.\) Sử dụng bất đẳng thức AM-GN, ta có:
\(2xy+x^2y^2\le x^2+y^2+x^2y^2\le x^2+y^2+z^2+x^2y^2+y^2z^2+z^2x^2=6\)
Từ đó suy ra: \(xy\le\sqrt{7}-1< 2\)
Chứng minh tương tự, ta cũng có:
\(yz< 2,\) \(zx< 2.\)
Do đó, ta có:
\(Q^2=x^2+y^2+z^2+2xy+2yz+2zx\ge x^2+y^2+z^2+x^2y^2+y^2z^2+z^2x^2=6\)
Hay: \(Q\ge\sqrt{6}\)
\(\Rightarrow Min_Q=\sqrt{6}\)
Cho x,y là hai số thực dương thay đổi thỏa mãn điều kiện ( x y + 1 ) ( x y + 1 - y ) ≤ 1 - x - 1 y . Tìm giá trị lớn nhất của biểu thức P = x + y x 2 - x y + 3 y 2 - x - 2 y 6 ( x + y )
A. 5 3 - 7 30
B. 7 30 - 5 3
C. 5 3 + 7 30
D. 5 + 7 30
Cho hai số thực c,y khác 0 thay đổi thỏa mãn điều kiện (x+y)xy=x2+y2-xy
Tính giá trị lớn nhất chủa biểu thức \(A=\frac{1}{x^3}+\frac{1}{y^3}\)
Ta có (x+y)xy=x2+y2-xy
=> \(\frac{1}{x}+\frac{1}{y}=\frac{1}{x^2}+\frac{1}{y^2}-\frac{1}{xy}\)
<=>\(\frac{1}{x}+\frac{1}{y}=\frac{1}{4}\left(\frac{1}{x}+\frac{1}{y}\right)^2+\frac{3}{4}\left(\frac{1}{x}-\frac{1}{y}\right)^2\ge\frac{1}{4}\left(\frac{1}{x}+\frac{1}{y}\right)^2\)
<=> \(0\le\frac{1}{x}+\frac{1}{y}\le4\)
mà \(A=\frac{1}{x^3+y^3}=\left(\frac{1}{x}+\frac{1}{y}\right)^2\le16\)
Vậy Max A =16 khi \(x=y=\frac{1}{2}\)
Cho x, y là hai số thực dương thay đổi và thỏa mãn điều kiện x + 2y - xy = 0. Tìm giá trị nhỏ nhất của biểu thức P = x 2 4 + 8 y + y 2 1 + x
A. 8 5
B. 5 8
C. 4 5
D. 5 4
Ta có
P = x 2 4 + 8 y + y 2 1 + x = x 2 4 + 8 y + 2 y 2 4 + 4 x ≥ x + 2 y 2 8 + 4 x + 2 y
Dấu “=” xảy ra khi x = 2y
Đặt t = x + 2y; t ≥ 8 . Khi đó P ≥ t 2 8 + 4 t
Xét hàm số f t = t 2 8 + 4 t , t ∈ [ 8 ; + ∞ )
Suy ra f(t) đồng biến trên [ 8 ; + ∞ ) nên f t ≥ f 8 = 8 5 Vậy m a x P = 8 5 ⇔ x = 4 ; y = 2
Đáp án A
Cho các số thực x, y, z thay đổi và thỏa mãn điều kiện x 2 + y 2 + z 2 = 1 . Giá trị nhỏ nhất của biểu thức P = x y + y z + 2 x z 2 − 8 x + y + z 2 − x y − y z + 2
A. min P = − 5
B. min P = 5
C. min P = 3
D. min P = − 3
Đáp án D
Ta có C 12 1 . C 10 1 = 120
Khi đó C 12 1 . C 10 1 = 120 . Đặt C 12 1 . C 10 1 = 120
Ta luôn có C 12 1 . C 10 1 = 120
C 12 1 . C 10 1 = 120 Suy ra C 12 1 . C 10 1 = 120
Xét hàm số f t = t 2 − 8 t + 3 trên khoảng − 1 ; + ∞ ,có f ' t = 2 t + 1 2 t + 4 t + 3 2 > 0 ; ∀ t > − 1
Hàm số f(t) liên tục trên − 1 ; + ∞ ⇒ f t đồng biến trên − 1 ; + ∞
Do đó, giá trị nhỏ nhất của f(t) là min − 1 ; + ∞ f t = f − 1 = − 3 . Vậy P min = − 3
Cho hai số thực x, y thay đổi thỏa mãn điều kiện x 2 + y 2 = 2 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = 2 ( x 3 + y 3 ) - 3 x y . Giá trị của của M + m bằng
A. -4
B. -1/2
C. -6
D. 1